Выберите серию
А можно ли отметить 10 клеток доски 5х5 так, чтобы в каждой полоске 1х3 содержалось не более одной отмеченной клетки?





Ответ:
Варианты ответов:
На доске 5х5 можно выделить 9 областей, в каждой из которых не более одной отмеченной клетки. Значит, всего таких клеток не более 9.

Можно ли отметить 8 клеток доски 5х5 так, чтобы в каждой полоске 1х3 содержалось не менее одной отмеченной клетки?





Ответ:
Варианты ответов:
Для решение этой задачи достаточно показать хотя бы один пример и проверить, что он подходит. Но как придумать такой пример?
Логично предположить, что в каждом прямоугольнике 1х3 ровно по одной отмеченной клетке. Тогда возникает диагональная раскраска в три цвета.

В такой раскраске синих клеток 9, а белых и красных – по 8. Значит, можно отметить, например, 8 красных клеток.
Плезно:
Определить, сколько полосок 1×3 можно провести по горизонтали и вертикали на доске 5×5.
Попробовать различные комбинации отмеченных клеток и проверьте, как они покрывают все полоски.
Можно использовать графический метод для визуализации – идея раскрасить доску в три цвета.
Идея диагонального смещения вертикальной полоски 1×3.
Проверить решение: убедиться, что в каждой полоске 1×3 есть хотя бы одна отмеченная клетка.
На доске $4\times4$ отмечены 4 клетки $х$.
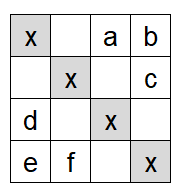
Какие две из клеток $a, b, c, d, e, f$ необходимо отметить, чтобы каждая полоска $1х3$, как вертикальная, так и горизонтальная содержала хоть одну отмеченную клетку?





Ответ:
Варианты ответов:
В каждой горизонтали можно выделить по 2 прямогольника $1х3$.
В верхней горизонтали – это тот прямогольник, который содержит клетку $x$ и тот прямогольник, который содержит клетку $b$. Эти прямоугольники имеют две общие клетки, среди которых отмеченных нет, так клетка $x$ является отмеченной. Значит, клетка $b$ тоже должна быть отмечена.
Во второй сверху горизонтали первый прямоугольник не содержит клетку $c$, в отличие от второго. Каждый из этих двух прямоугольников содержит отмеченную клетку. Значит, $c$ не должна быть отмеченной.
Аналогичным образом, можно доказать, что $d$ и $f$ не должны быть отмечены, а клетка $e$ должна быть отмечена.
Можно ли на доске $8\times8$ отметить 8 клеток так, чтобы любая горизонтальная полоска $1\times5$ содержала отмеченную клетку?





Ответ:
Варианты ответов:
Да, вот пример, где x соответствуют отмеченной клетке.
o o o x o o o o
o o o x o o o o
o o o x o o o o
o o o x o o o o
o o o x o o o o
o o o x o o o o
o o o x o o o o
o o o x o o o o
Можно ли на доске $8\times8$ отметить 7 клеток так, чтобы любая горизонтальная полоска $1\times5$ содержала отмеченную клетку?





Ответ:
Варианты ответов:
В каждой горизонтали доски $8\times8$ выделим по 1 прямоугольнику $1\times5$.
Получим 8 прямоугольников, в каждом из которых нужно отметить не менее одной клети. Значит, отметить 7 клеток указанным образом нельзя.
Другое решение: Предположим нам удалось отметить 7 клеток указанным образом. Тогда, так как строк 8, а отмеченных клеток всего 7, то найдётся строка в которой нет отмеченных клеток. В этой строке без труда найдем полоску длины 5, в которой нет отмеченных клеток.