Выберите серию
Из доски 5х5 вырезали одну клетку и остаток удалось разрезать на полоски 1х3. Какая клетка могла быть вырезана?





Ответ:
Варианты ответов:
Рассмотрим диагональную раскраску в три цвета.

Каждый прямоугольник 1x3 при такой раскраске занимает по одной клетке каждого цвета. Но на доске синих клеток на красных и белых клеток по 8, а синих – 9. Значит, вырезали синюю клетку.
Повернём раскраску на 90 градусов. Получим ещё одну диагональную раскраску в три цвета. На этот раз *все синие клетки, кроме одной,* окажутся в новых местах.

Значит, вырезать могли только ту клетку, которая оказалась синей оба раза. Это центральная клетка *c3*.
С помощью раскраски покажите, что если вырезать клетку B или C, то остаток не получится разрезать на полоски 1х3.
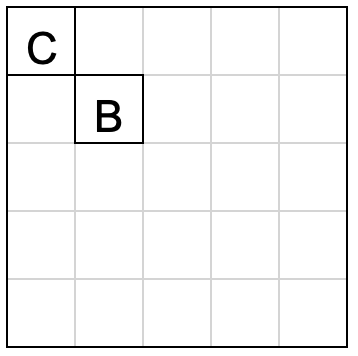
Выберите раскраски, которые могут помочь в этом.









Ответ:
Варианты ответов:
Занумеруем рисунки с раскрасками слева направо числами от 1 до 4. Раскрасим доску в три цвета диагональной раскраской двумя способами, как указано на рисунках №2 и №4.
Каждый прямоугольник 1x3 занимает по одной клетке каждого цвета. Значит, в разбиении из 24-х клеток, оставшихся после удаления одной из двух клеток B или С на доске остаётся должно быть по 8 клеток каждого цвета. Для второй раскраски это условие выполняется. А для четвёртой – нет. В ней синих клеток 9.
Осталось заметить, что раскраски №1 и №3 не имеют закономерностей, характерных для прямоугольников 1x3.
При решении этой задачи полезно:
1) Обратить внимание на то, как вырезание клеток B или C влияет на возможность разрезания оставшихся клеток на полоски 1×3.
2) Использовать идею диагональной раскраски.
С помощью раскраски покажите, что если вырезать из доски 5 на 5 клетку A, как это указано на рисунке слева, то остаток не получится разрезать на полоски 1х3.
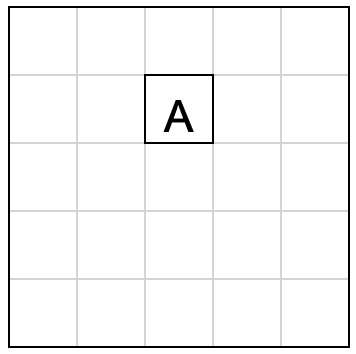


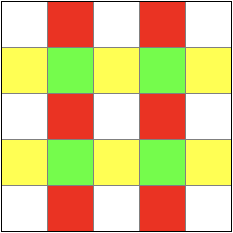

Выберите подходящую раскраску из перечисленных.





Ответ:
Варианты ответов:
Для первых трёх ракрасок нет закономерностей на полосках 1х3.
1) В шахматной раскраске такая полоска может занимать как 1 белую клетки, так и 2.
2) В раскраске матрас полоска 1х3 может занимать как 3 белые клетки, так и ни одной.
3) В четырёхцветной раскраске полоска может занимать как 2 клетки одного цвета и 1 другого.
4) А в трёхцветной диагональной раскраске полоска 1х3 *всегда* занимает три клетки разных цветов. Если бы после удаления одной клетки доску 5х5 *можно было бы* разрезать на полоски из трёх клеток, то клеток каждого цвета было бы по (25-1):3=8.
Всего на доске при этом 9 синих, по 8 белых и красных клеток. Если удалить белую клетку A, то синих клеток будет всё ещё 9. То есть клеток разных цветов не поровну. Значит, разрезать оставшиеся 24 клетки на полоски из трёх клеток нельзя.
Дана шахматная раскраска и прямоугольник из 2 клеток - домино.

Сколько клеток белого цвета может занимать одна такая фигура при шахматной раскраске?





Ответ:
Варианты ответов:
При любом допустимом положении домино занимает две клетки. Эти клетки разных цветов, так как они имеют общую сторону. Значит, фигура домино занимает на шахматной доске всегда по одной клетке каждого цвета.
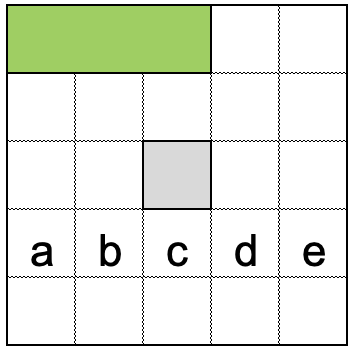
Из доски 5х5 вырезали центральную клетку и начали разрезать на полоски 1х3. Закончите разрезание. Вместе с каким клетками в одной полоске окажется клетка с?





Ответ:
Варианты ответов:
Рассмотрим клетки 1 и 2. Они должны быть в вертикальных прямоугольниках $1\times 3$. Значит, клетка 3 в горизонтальном. Клетки e и 4 – тоже в горизонтальных прямоугольниках. Осталось завершить разрезание двумя вертикальным прямоугольниками, содержащими клетки a и b.
