Выберите серию
Из квадрата 3 на 3 вырезали одну клетку двумя разными способами.
Получились две фигуры:
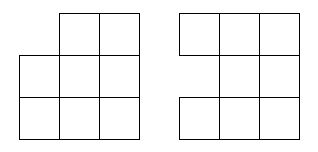
Какую из них можно разрезать на домино?





Ответ:
Варианты ответов:
Из доски 8х8 вырезали одну клетку и остаток удалось разрезать на полоски 1х3. Какая клетка могла быть вырезана?
В ответ укажите клетку доски в формате е2, где е – обозначение вертикали, а 2 – номер горизонтали. Например, одна из угловых клеткок – это a1, противоположная ей h8, две другие угловые это a8 и h1.
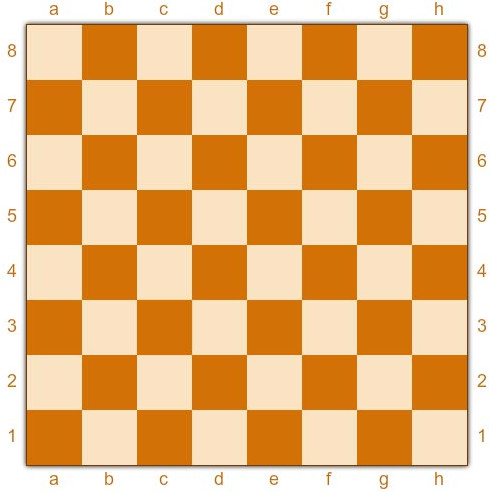





Ответ:
Варианты ответов:
Рассмотрим 2 диагональные раскраски в три цвета. Каждая полоска 1х3 для таких раскрасок занимает по одной клетке белого, синего и красного цвета.


При каждой из раскрасок на доске белых клеток 21, красных тоже 21, а синих 22.
Значит, вырезанная клетка должна быть синей на каждой из раскрасок. Получаем 4 клетки, которые под подозрением: c3, f3, c6, f6. Осталось убедиться, что для каждой из них есть способ разбиения оставшейся части доски на полоски 1х3. Но такой способ уже был в решении предыдущей задачи.
ПРи решении этой задачи полезно использовать идею диагональной раскраски в 3 цвета. Далее посчитайте, сколько клеток каждого цвета получилось, как могут располагаться полоски 1х3 (каждая полоска содержит клетки трех разных цветов)
Разрежьте доску 8х8 без указанной клетки на прямоугольники 1х3. Как объяснить, что необходимо сделать не менее 21 выстрела по доске 8х8, чтобы попасть в корабль 1х3?
Выберите верный вариант ответа:
а) каждый из 21 прямоугольников нужно проверить;
б) в каждый из 21 кораблей нужно сделать выстрел;
в) $63=21\cdot 3$, значит нужно сделать 21 выстрел.





Ответ:
Варианты ответов:
Вот один из способов, как оставшуюся часть доски можно разбить на прямоугольники 1x3.

При этом в каждом таком прямоугольнике нужно проверить хотя бы одну клетку, иначе в этом прямоугольнике может оказаться корабль 1х3.
Какое наименьшее число выстрелов надо сделать по доске 8х8 чтобы гарантированно попасть в корабль 1х4?





Ответ:
Варианты ответов:
Рассмотрим диагональную раскраску в 4 цвета.

Каждый корабль 1х4 занимает по одной клетке белого, красного, зелёного и синего цветов. Значит, к примеру, достаточно проверить все синие клетки. Их 16.
Осталось доказать, что меньше, чем за 16 выстрелов, гарантированно попасть в корабль 1х4 нельзя. Разрежем доску на 16 прямоугольников, по 2 в каждой строке. Если не проверить хотя бы один из них, то в нём может оказаться корабль 1х4. Значит, нужно не менее 16 выстрелов.
Полезно:
1) Использовать идею диагональной раскраски.
2) Определить возможные позиции для корабля 1×4 и как они могут располагаться на доске. Как он раскрашен? В клетки какого цвета достаточно попасть, чтобы попасть в корабль? Сколько таких клеток?
На доске 5х5 расположен трёхпалубный корабль 1х3. Вася сделал 5 выстрелов по диагонали в клетки x. Какие 4 выстрела надо сделать, чтобы быть уверенным, что попал в корабль хоть раз? Результат попадания виден со спутника только после всех выстрелов.
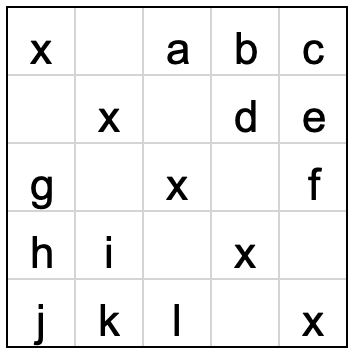





Ответ:
Варианты ответов:
Применим диагональную раскраску в 3 цвета.

Каждый трёхпалубный корабль при такой раскраске занимает по одной клетке каждого цвета. Вася проверил 5 синих клеток главной диагонали. Значит, он может проверить ещё 4 синие клетки.
Докажем, что если хотя бы одна из указанных синих клеток b, e, h или k не проверена, то найдётся место для трёхпалубного корабля. Например, если Вася не проверил клетку b.
Все непроверенные клетки разбиваются на 2 части – одна над главной диагональю, а вторая – под ней. *Среди клеток под диагональю* нужно проверить хотя бы 2 клетки – по одной в каждом из двух отмеченных жёлтых прямоугольников 1x3. Иначе найдётся трёхпалубный корабль, который Вася не подбил.
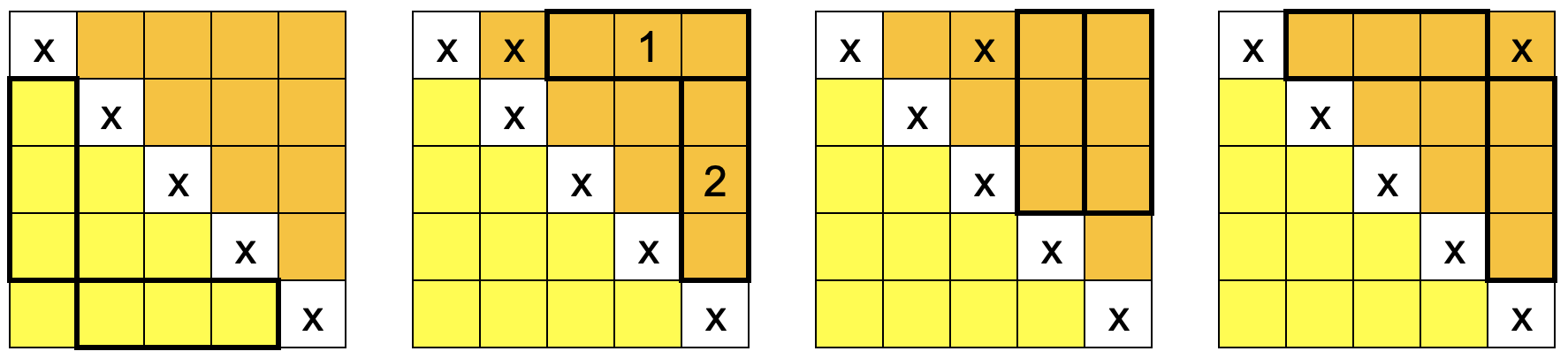
*Для клеток над диагональю* рассуждения иные. Рассмотрим верхнюю строку. Кроме одной отмеченной клетки Васе нужно проверить ещё хотя бы одну клетку в этой строке. Если это не клетка b, то возможны три случая. В каждом из них найдётся по два оранжевых прямоугольника 1x3, в которых могут быть трёхпалубные корабли. Васе потребуется отметить не менее 3 клеток над диагональю.
Таким образом, если Вася не проверил клетку b, то ему нужно проверить не менее 5 клеток.
Значит, ровно 4 клетки Вася может проверить только одним способом.