Выберите серию
На доске $4х4$ нельзя отметить 7 клеток так, чтобы каждый прямоугольник 1х2 содержал отмеченную клетку.
*Восстановите доказательство.*
Разобьём доску на прямоугольники $1\times$__ так, что в каждом из них должна быть отмечена хотя бы одна клетка.
Всего их получится __.
Значит, всего отметить придётся не менее __ клеток.
А требовалось отметить __ клеток. Значит, это невозможно.
Ответ:
Варианты ответов:
Разобьём доску на прямоугольники $1\times2$.
Всего их получится 8 штук. В каждом таком прямоугольнике должна быть отмечена хотя бы одна клетка.
Значит, всего отметить придётся не менее 8 клеток.
А требовалось отметить 7 клеток. Значит, это невозможно.
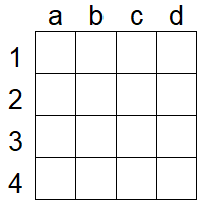
На доске $4\times4$ необходимо отметить 8 клеток так, чтобы каждый прямоугольник 1х2 содержал одну клетку. В ответ через пробел укажите координаты 8 клеток, одна из которых a1.
Ответ:
Варианты ответов:
Рассмотрим прямоугольник из пары клеток (a1, a2). Так как клетка a1 отмечена, то клетку a2 отмечать нельзя. Значит в прямоугольнике из пары клеток (a2, a3) клетку a3 нужно отметить обязательно. Аналогичным образом, рассматривая пары (a3, a4), (a4, a8), (a8, a7), и т.д. получаем 8 отмеченных клеток.
Если посмотреть на шахматную раскраску этой доски, то можно взять все клетки одного цвета: a1, a3, b2, b4, c1, c3, d2 и d4 или a2, a4, b1, b3, c2, c4, d1 и d3 в зависимости от того, отмечена клетка a1 или нет.
На дне рождения каждый мальчик съел 4 конфеты, 4 котлеты и 4 козинака, а каждая девочка съела 10 конфет, 3 котлеты и 24 козинака. Всего было съедено 714 конфет и 371 котлета. Сколько было съедено козинаков?
Ответ:
Варианты ответов:
В течение недели ученик каждый день решал на две задачи больше, чем в предыдущий день, при этом в воскресенье он решил втрое больше задач, чем в понедельник. Сколько задач он решил в пятницу?
Ответ:
Варианты ответов:
В большую квадратную комнату внесли два квадратных ковра. Сторона одного из ковров в два раза больше стороны другого. Оказалось, что если положить ковры в противоположные углы комнаты, то они покроют в два слоя участок пола площадью 4м$^2$. А если положить ковры в соседние углы комнаты, то в два слоя окажется покрыт участок площадью 14м$^2$. Чему равна сторона комнаты?
Ответ:
Варианты ответов: