Выберите серию
Восстановите решение задачи *раскраски10*
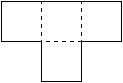
Пусть у кто-то смог разбить квадрат $6\times6$ на "тетраминошки".
Тогда квадрат из 36 клеток должен разбиться ровно на __ фигурок из четырех клеток.
Заметим, что при шахматной раскраске, каждая такая фигурка содержит в себе
либо 3 белые и 1 черную клеточку,
либо 3 черных и 1 белую.
Рассмотрим белые клетки: в каждой фигурке их количество (чётное - Ч или нечётное - Н) __ .
Всего фигурок 9, значит общее количество белых клеток будет нечетным (сумма нечетного количества нечетных чисел - нечетна), но по раскраске количество белых клеток у нас (чётное - Ч или нечётное - Н) __ .
Получили противоречие, значит невозможно разбить квадрат таким образом.
Ответ:
Варианты ответов:
Докажите, что квадрат $6\times6$ нельзя разбить на фигуры из четырёх клеток T-тетрамино.
Какая из предложенных раскрасок может помочь при этом?
Ответ:
Варианты ответов:
Верное решение с помощью первой раскраски можно восстановить в следующей задаче.
Отметим, что во второй раскраске возможны тетрамино, содержащие как по 1, как по 2, так и по 3 черных клетки, то есть никакого общего рассуждения провести нельзя.
Третья раскраска также не позволяет получить противоречия, так как тетрамино занимает в разных случаях от 0 до 2 клеток каждого из четырёх цветов.
Восстановите решение задачи *раскраски07*.
*Условие задачи.*
_Докажите, что квадрат $6\times6$ нельзя разбить на прямые тетрамино._
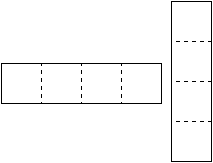
*Решение задачи.*
Пусть кто-то смог разбить квадрат $6\times6$ на прямые тетрамино.
Рассмотрим диагональную раскраску в 4 цвета. Каждая фигура тетрамино занимает при такой раскраске фиксированное количество белых клеток. А именно __.
Квадрат из 36 клеток должен разбиться ровно на __ фигурок из четырех клеток.
Заметим, что при выбранной раскраске, каждая такое тетрамино содержит в себе по 1 клетке каждого цвета.
Учитывая общее количество тетрамино, красных клеток должно быть __,
но согласно раскраске количество красных клеток равно __ .
Получили противоречие, значит невозможно разбить квадрат таким образом.
Ответ:
Варианты ответов:
Восстановите решение задачи *раскраски07*.
*Условие задачи.*
_Докажите, что квадрат $6\times6$ нельзя разбить на прямые тетрамино._
*Решение задачи.*
Пусть кто-то смог разбить квадрат $6\times6$ на прямые тетрамино.
Тогда квадрат из 36 клеток должен разбиться ровно на __ фигурок из четырех клеток.
Заметим, что при шахматной раскраске квадратами 2 на 2, каждая такая фигурка содержит в себе 2 белые клетки.
Учитывая общее количество тетрамино, белых клеток должно быть __,
но согласно раскраске количество белых клеток __ .
Получили противоречие, значит невозможно разбить квадрат таким образом.
Ответ:
Варианты ответов:
Докажите, что квадрат $6\times6$ нельзя разбить на прямые тетрамино.
Какая из предложенных раскрасок может помочь при этом?
Ответ:
Варианты ответов:
Шахматная раскраска не позволит получить противоречия, так как при ней на доске получается по 18 клеток белого и чёрного цветов. А каждое из 9 прямых тетрамино как раз занимает по 2 клетки тех же цветов.
Решения для второй и третьей раскраски можно восстановить в следующих двух задачах.