Однажды каждый из 1000 островитян сказал: «Среди остальных 999 жителя острова есть по меньшей мере один лжец». Сколько рыцарей живет на острове?

В комнате находится пятеро островитян. Серёжа сказал Никите, а потом Вите: "Ты рыцарь." После этого он сказал Саше, а затем Паше: "Ты лжец!" Что скажет Паша про остальных?

Серёже: "Ты __"

Никите: "Ты __"

Вите: "Ты __"

Саше: "Ты __"

Путешественник, попавший на остров Рыцарей и Лжецов, встретил четырех людей и задал им вопрос: "Кто вы?". Известно, что среди них обязательно есть хотя бы один рыцарь и хотя бы один лжец. Он получил такие ответы: Первый: "Все мы лжецы". Второй: "Среди нас один лжец". Третий: "Среди нас два лжеца". Четвёртый: "Я ни разу не соврал и сейчас не вру". Кем является каждый из них? Если невозможно определить, кем является житель, напишите "неизвестно".

Первый: __

Второй: __

Третий: __

Четвёртый: __

Три мальчика-островитянина разговаривают после урока:

Антон: Я получил за контрольную 5!

Борис: Я написал работу не хуже, чем Вадим.

Вадим: Антон написал контрольную на 4.

Антон: Кстати, Борис написал её на 4.

Борис: Вадим получил 4.

Вадим: Я получил 5.

Известно, что среди этих мальчиков ровно один лжец Определите, кто из них написал контрольную работу на 4.

В комнате три островитянина. Первый сказал: «В комнате один рыцарь», второй ответил: «Нет, в комнате два рыцаря!», третий заявил: «В комнате все рыцари!». Сколько рыцарей может быть в комнате?

Однажды в четверг после дождя между островитянами Тимом и Томом произошел следующий диалог:

– Ты можешь сказать, что я рыцарь, – гордо заявил Тим.

– Ты можешь сказать, что я лжец, – грустно ответил ему Том.

Кем являются Тим и Том?

Тим: __

Том: __

По кругу сидит 12 островитян. Каждый из них видит всех, за исключением своих соседей и, конечно, себя. Все люди по очереди сказали: <<Все, кого я вижу – лжецы>>. Сколько рыцарей сидит за столом?

За круглым столом сидят 7 островитян. Каждый из сидящих за столом сказал: <<Мои соседи – лжец и рыцарь>>. Определите, сколько среди них лжецов.

Собралась компания островитян разного роста. Каждый заявил «Среди тех, кто выше меня, есть лжецы». Сколько лжецов могло быть среди них?

Как-то раз встретились два островитянина и первый сказал второму: «По крайней мере один из нас – лжец». История умалчивает, ответил ли ему на это что-либо собеседник. Тем не менее определите, кем являются оба.

Первый: __

Второй: __

Встретились несколько островитян, и каждый заявил всем остальным: «Вы все — лжецы». Сколько рыцарей было среди них?

Один из островитян сказал другому: «По крайней мере один из нас — рыцарь». «Ты — лжец», — ответил ему второй. Кто из них кто?

Первый: __

Второй: __

Собрались двое островитян. Первый сказал: "По крайней мере один из нас лжец". Кто из них кто?

Первый __

Второй __

Собрались двое островитян. Первый сказал: "Мы оба лжецы". Кто из них кто?

Первый __

Второй __

Решите ребус: БАО$\cdot$ БА$\cdot$ Б =2002.

Б=__, А=__, О=__.

Дан ребус ДУБ + ДУБ + . . . + ДУБ = ЛЕС. Какое наибольшее число дубов может быть в лесу?

Сумма МАДАМ + МАДАМ + ... + МАДАМ (99 999 слагаемых) оканчивается на 679. Чему равно МАДАМ?

Дан ребус ЗИМА+СКОРО=ПРИДЕТ. Чему может соответствовать буква Т?

а) 0, б) 1, в) 3, г) 7, д) ни одной из перечисленных цифр.

В ребусе КРОСС+КРОСС=СПОРТ буква Р может соответствовать цифре:

а) 0, б) 2, в) 4, г) 5, д) 6.

В ребусе ВАСЯ+ПЕТЯ=ТОПОТ буква Т может соответствовать цифре:

а) 1, б) 2, в) 4, г) 8, е) ни одной из перечисленных.

Дан ребус КОТ+РОГ=ВОЛ. Чему может быть равна О? Перечислите все варианты.

Решите ребус ДА+ДА+ДА=ЕДА.

Е=__, Д=__, А=__.

Сколько решений имеет ребус КВА+КВА=ЖАБА?

Дан ребус КВА+КВА=ЖАБА. Найдите А.

Дан ребус КВА+КВА=ЖАБА. Найдите Ж.

Восстановите решение задачи *раскраски10*

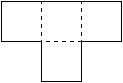
Пусть у кто-то смог разбить квадрат $6\times6$ на "тетраминошки".
Тогда квадрат из 36 клеток должен разбиться ровно на __ фигурок из четырех клеток.

Заметим, что при шахматной раскраске, каждая такая фигурка содержит в себе
либо 3 белые и 1 черную клеточку,
либо 3 черных и 1 белую.
Рассмотрим белые клетки: в каждой фигурке их количество (чётное - Ч или нечётное - Н) __ .

Всего фигурок 9, значит общее количество белых клеток будет нечетным (сумма нечетного количества нечетных чисел - нечетна), но по раскраске количество белых клеток у нас (чётное - Ч или нечётное - Н) __ .

Получили противоречие, значит невозможно разбить квадрат таким образом.

Докажите, что квадрат $6\times6$ нельзя разбить на фигуры из четырёх клеток T-тетрамино.

Какая из предложенных раскрасок может помочь при этом?

Восстановите решение задачи *раскраски07*.

*Условие задачи.*

_Докажите, что квадрат $6\times6$ нельзя разбить на прямые тетрамино._

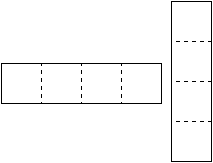
*Решение задачи.*

Пусть кто-то смог разбить квадрат $6\times6$ на прямые тетрамино.

Рассмотрим диагональную раскраску в 4 цвета. Каждая фигура тетрамино занимает при такой раскраске фиксированное количество белых клеток. А именно __.

Квадрат из 36 клеток должен разбиться ровно на __ фигурок из четырех клеток.

Заметим, что при выбранной раскраске, каждая такое тетрамино содержит в себе по 1 клетке каждого цвета.

Учитывая общее количество тетрамино, красных клеток должно быть __,

но согласно раскраске количество красных клеток равно __ .

Получили противоречие, значит невозможно разбить квадрат таким образом.

Восстановите решение задачи *раскраски07*.

*Условие задачи.*

_Докажите, что квадрат $6\times6$ нельзя разбить на прямые тетрамино._

*Решение задачи.*

Пусть кто-то смог разбить квадрат $6\times6$ на прямые тетрамино.
Тогда квадрат из 36 клеток должен разбиться ровно на __ фигурок из четырех клеток.

Заметим, что при шахматной раскраске квадратами 2 на 2, каждая такая фигурка содержит в себе 2 белые клетки.

Учитывая общее количество тетрамино, белых клеток должно быть __,

но согласно раскраске количество белых клеток __ .

Получили противоречие, значит невозможно разбить квадрат таким образом.

Докажите, что квадрат $6\times6$ нельзя разбить на прямые тетрамино.

Какая из предложенных раскрасок может помочь при этом?