Все задачи
Условие
Даны три раскрасски:
а) шахматная;
б) шахматная 2 на 2;
в) трёхцветная диагональная;
и прямоугольник из 4 клеток - прямое тетрамино.



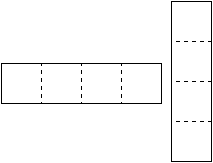
На каких раскрасках прямое тетрамино занимает обязательно 2 белых клетки?
Условие
Дана шахматная раскраска и прямоугольник из 4 клеток - прямое тетрамино.


Сколько клеток белого цвета может занимать одна такая фигура при шахматной раскраске?
Условие
Дана шахматная раскраска и фигура из четырёх клеток в форме буквы T - тетрамино.

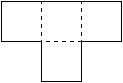
Сколько клеток белого цвета может занимать данная фигура?
Условие
Из квадрата 4 на 4 вырезали две клетки двумя разными способами.
Получились две фигуры:
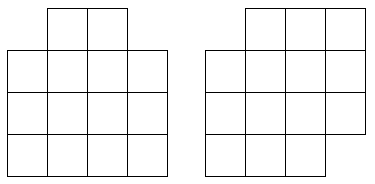
Какую из них нельзя разрезать на домино?
Условие
Из квадрата 3 на 3 вырезали одну клетку двумя разными способами.
Получились две фигуры:
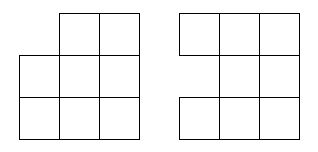
Какую из них можно разрезать на домино?
Условие
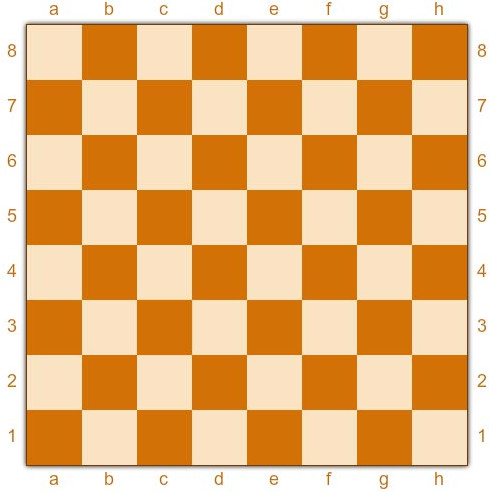
Из доски 8х8 вырезали одну клетку и остаток удалось разрезать на полоски 1х3. Какая клетка могла быть вырезана?
В ответ укажите клетку доски в формате е2, где е – обозначение вертикали, а 2 – номер горизонтали. Например, одна из угловых клеткок – это a1, противоположная ей h8, две другие угловые это a8 и h1.
Условие
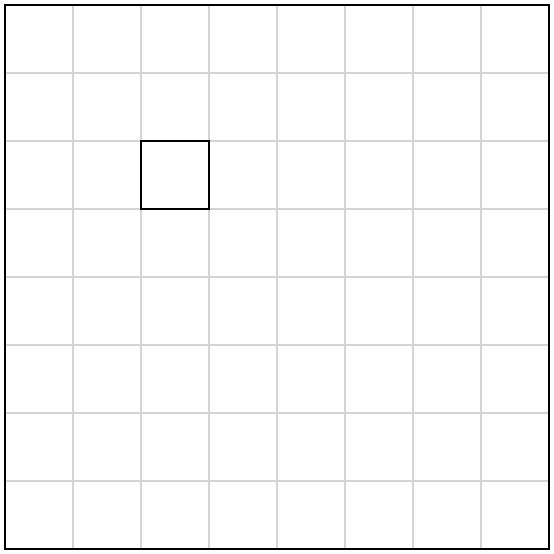
Разрежьте доску 8х8 без указанной клетки на прямоугольники 1х3. Как объяснить, что необходимо сделать не менее 21 выстрела по доске 8х8, чтобы попасть в корабль 1х3?
Выберите верный вариант ответа:
а) каждый из 21 прямоугольников нужно проверить;
б) в каждый из 21 кораблей нужно сделать выстрел;
в) $63=21\cdot 3$, значит нужно сделать 21 выстрел.
Условие
Какое наименьшее число выстрелов надо сделать по доске 8х8 чтобы гарантированно попасть в корабль 1х4?
Условие
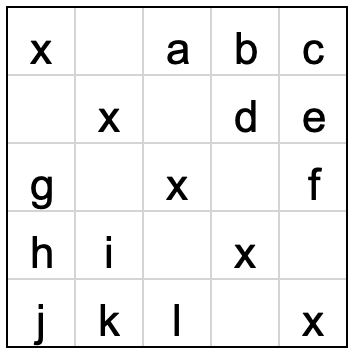
На доске 5х5 расположен трёхпалубный корабль 1х3. Вася сделал 5 выстрелов по диагонали в клетки x. Какие 4 выстрела надо сделать, чтобы быть уверенным, что попал в корабль хоть раз? Результат попадания виден со спутника только после всех выстрелов.
Условие
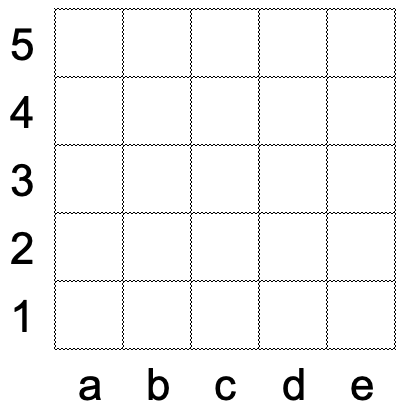
Из доски 5х5 вырезали одну клетку и остаток удалось разрезать на полоски 1х3. Какая клетка могла быть вырезана?
Условие
С помощью раскраски покажите, что если вырезать клетку B или C, то остаток не получится разрезать на полоски 1х3.
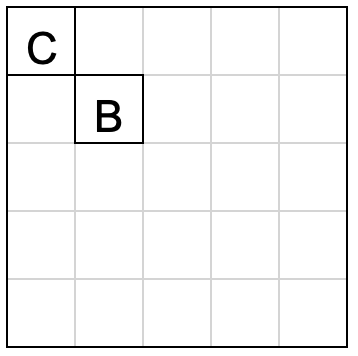
Выберите раскраски, которые могут помочь в этом.




Условие
С помощью раскраски покажите, что если вырезать из доски 5 на 5 клетку A, как это указано на рисунке слева, то остаток не получится разрезать на полоски 1х3.
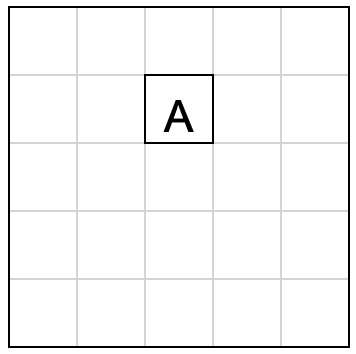


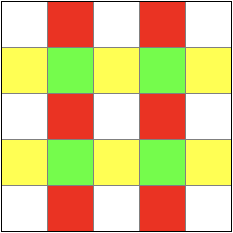

Выберите подходящую раскраску из перечисленных.
Условие
Дана шахматная раскраска и прямоугольник из 2 клеток - домино.

Сколько клеток белого цвета может занимать одна такая фигура при шахматной раскраске?
Условие
Из доски 5х5 вырезали центральную клетку и начали разрезать на полоски 1х3. Закончите разрезание. Вместе с каким клетками в одной полоске окажется клетка с?
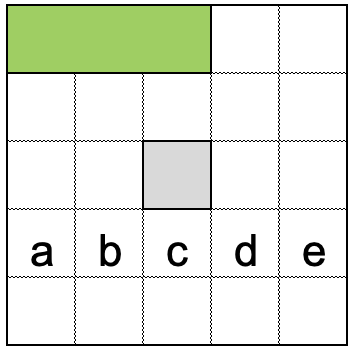
Условие
А можно ли отметить 10 клеток доски 5х5 так, чтобы в каждой полоске 1х3 содержалось не более одной отмеченной клетки?
Условие
Можно ли отметить 8 клеток доски 5х5 так, чтобы в каждой полоске 1х3 содержалось не менее одной отмеченной клетки?
Условие
На доске $4\times4$ отмечены 4 клетки $х$.
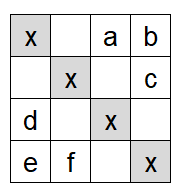
Какие две из клеток $a, b, c, d, e, f$ необходимо отметить, чтобы каждая полоска $1х3$, как вертикальная, так и горизонтальная содержала хоть одну отмеченную клетку?
Условие
Можно ли на доске $8\times8$ отметить 8 клеток так, чтобы любая горизонтальная полоска $1\times5$ содержала отмеченную клетку?
Условие
Можно ли на доске $8\times8$ отметить 7 клеток так, чтобы любая горизонтальная полоска $1\times5$ содержала отмеченную клетку?
Условие
Какое наименьшее число клеток доски $8\times8$ необходимо отметить, чтобы каждый прямоугольник $1\times2$ содержал отмеченную клетку?
Условие
На доске $4х4$ нельзя отметить 7 клеток так, чтобы каждый прямоугольник 1х2 содержал отмеченную клетку.
*Восстановите доказательство.*
Разобьём доску на прямоугольники $1\times$__ так, что в каждом из них должна быть отмечена хотя бы одна клетка.
Всего их получится __.
Значит, всего отметить придётся не менее __ клеток.
А требовалось отметить __ клеток. Значит, это невозможно.
Условие
На доске $4\times4$ необходимо отметить 8 клеток так, чтобы каждый прямоугольник 1х2 содержал одну клетку. В ответ через пробел укажите координаты 8 клеток, одна из которых a1.
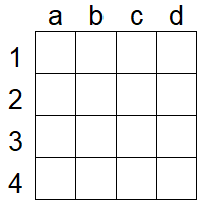
Условие
Условие
Условие
Условие
Найдите все натуральные числа $N$ такие, что ровно два из трёх чисел $N$, $N+3$, $N+5$ являются трёхзначными.
Условие
Придумайте пять различных двузначных нечётных чисел с суммой 77. В ответ запишите самое большое и самое маленькое из них. Только два числа!
Условие
Условие
Условие
В $2052$ году в марте будет больше воскресений, чем понедельников. На какой день выпадет 1 апреля в том году?