Все задачи
Условие
Чему равна разность периметров красной и синей фигур? (длину стороны клетки считаем равной 1)
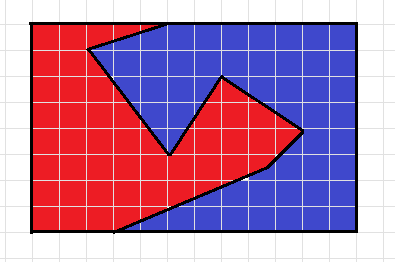
Условие
Найдите периметр многоугольника (длину стороны клетки принимаем за 1).
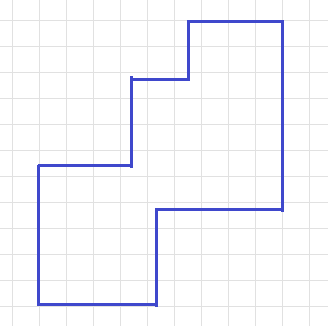
Условие
Чему равна площадь синего "сапога"? (площадь одной клетки принимаем за 1)
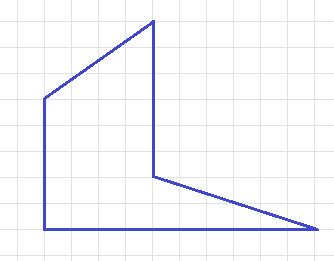
Условие
Забор (на плане показан зеленым) ограничивает шестиугольный участок. Найдите площадь этого участка (в квадратных метрах), если площадь одной клетки равна 25 кв. м.
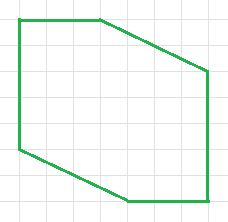
Условие
Со дня города Майкопа четыре школьника начали посещать Математический Парк. Первый бывал в нём каждый четвёртый день, второй – каждый пятый, третий – каждый шестой и четвёртый – каждый девятый. Через сколько дней все школьники встретятся в этом парке?

Парк находится по адресу ул. Советская 180.
Условие
По одной из версий название Майкопа происходит от адыгского слова Мыекъуапэ. Что переводится как *долина яблонь*.
Настоящий садовод всегда хорошо продумывает тропинки в саду.
Вот схема одного из садов, где среди нескольких тропинок растёт одна яблоня.

Посадите ещё три яблони так, чтобы по обе стороны от каждой тропинки было поровну яблонь.
Какие области нужно выбрать при этом? Укажите их номер через пробел в порядке возрастания.
Условие
Что общего у Майкопа с Москвой?
В Москве площадь "Дружба народов" расположена на ВДНХ (Выставка достижений народного хозяйства) вокруг фонтана «Дружба народов» и имеет четкую восьмиугольную форму, как и чаша самого фонтана.

Мемориальный комплекс площадь «Дружбы» в городе Майкоп расположен по соседству с поющими фонтанами, соборной мечетью, филармонией и Адыгейской республиканской гимназией.

Однажды жители Майкопа заметили, что фонтан на *Площади дружбы народов* включают по вторникам, пятницам и нечётным числам. Какое наибольшее количество дней подряд можно было наслаждаться фонтаном?
Условие
Мировую известность Майкоп обрел после того, как в 1897 году здесь был открыт курган «Ошад» – захоронение скифско-сарматского периода, в котором обнаружили множество золотых и серебряных изделий. Сколько лет прошло с тех пор?

Условие
Майко́п — город на юге России. Столица Республики Адыгея. Дата основания города - 25 мая 1857 года. День города в 2023 году отмечался 2 сентября. Сколько лет отмечал Майкоп в этом году?
Условие
На острове Логики живут рыцари (всегда говорящие правду), лжецы (всегда говорящие неправду) и софисты. Софист может произносить только такие фразы, которые на его месте не смогли бы сказать ни рыцарь, ни лжец. Например, стоя рядом со лжецом, софист может сказать фразу <<Мы оба лжецы>> (потому что если бы он был рыцарем, то такая фраза была бы ложью, а если бы он был лжецом, она была бы истиной).
Однажды софист произнёс три утверждения о жителях острова:
1. На острове живут ровно 25 лжецов.
2. На острове живут ровно 26 рыцарей.
3. Софистов на острове не меньше, чем рыцарей.
Сколько всего человек живут на острове?
Условие
В галактике Кин-Дза-Дза живут пацаки и чатлане. У них принято говорить правду, если в помещении присутствуют представители обеих рас, и врать среди своих. Собрались в комнате трое жителей планеты. Первый сказал: <<Я пацак>>, и вышел из помещения. Второй сказал: <<А я чатланин>>. Определите, кем является каждый из них. Не забудьте доказать, что другие варианты невозможны.
Первый __, второй __, третий __
Условие
В комнате находятся три человека разных типов: рыцарь (всегда говорит правду), лжец (всегда лжёт) и хитрец (может говорить всё, что хочет). Первый из них сказал, что остальные два одного типа, второй – что остальные двое разных типов, а третий – что первый хитрец. Кто из них к какому типу относится?
Первый __, второй __, третий __
Условие
На острове есть две деревни. В одной из них живут рыцари,
которые всегда говорят правду, а в другой --- лжецы, которые всегда лгут.
Трое жителей острова --- A, B и C --- собрались вместе и произнесли:
--- И B, и C говорят правду, --- сказал A.
--- Хотя бы один из A и C говорит правду, --- сказал B.
Найдите среди них тех, кто гарантированно из одной деревни.
Условие
В круг встало несколько индейцев и несколько бледнолицых - всего 100 человек. Индейцы говорят правду индейцам и лгут бледнолицым, а бледнолицые говорят правду бледнолицым и лгут индейцам. Каждый сказал своему соседу справа: <<Ты индеец>> или: <<Ты бледнолицый>>. Известно, что было произнесено 40 фраз <<Ты индеец>>. Сколько было бледнолицых?
Условие
Из пятерых детей некоторые всегда говорят правду, а остальные всегда лгут. Серёжа сказал Никите, а потом Вите: <<Ты правдивый парень.>> После этого он сказал Саше, а затем Паше: <<Ты лгун!>> Кого из перечисленных назовёт лгуном Паша?
Условие
На доске написано двузначное число, а Петя, Вася и Коля пытаются поделить это число.
Петя: это число делится на 8, на 3 и на 5.
Вася: это число делится на 3, на 7 и на 8.
Коля: это число делится на 7, на 5 и на 8.
Известно, что каждый мальчик два раза ошибся и один раз сосчитал верно. Выясните, каким могло быть это число (приведите все варианты).
Условие
Петя, Коля, Саша и Игорь заняли первые четыре места в соревнованиях по лузганью семечек. В качестве приза за первое место выдали 4 мешка семечек, за второе --- 3, за третье --- 2, а за четвертое --- 1 мешок. Известно, что Петя, Саша и Игорь вместе получили меньше 9 мешков; Коля, Саша, Игорь --- меньше 8 мешков; Петя, Коля и Саша --- меньше 7 мешков. Определите, какое место занял каждый из ребят (напишите словами).
Петя __, Коля __, Саша __, Игорь __
Условие
Дима, Саша, Коля, Глеб выступили на олимпиаде и заняли первые четыре места. Через год их одноклассникам по обрывочным данным удалось восстановить лишь три факта: <<Дима занял первое место или Глеб --- третье>>, <<Глеб занял второе место или Коля --- первое>>, <<Саша занял третье место или Дима --- второе>>. Кто выступил лучше --- Дима или Саша?
Условие
В вазочку положили несколько конфет. Трое мальчиков их сосчитали и
по очереди сказали: <<Тут больше девяти конфет>>, <<Конфет больше
пятнадцати>>, <<Конфет в вазочке меньше двенадцати>>. При этом ровно один
из них ошибся. Какое наименьшее количество конфет могло лежать в вазочке?
Условие
Перед началом урока учитель написал на доске какое-то целое число от 1 до 10. После этого дети по очереди сказали следующее:
Первый: <<Это число больше 1.>>
Второй: <<Это число больше 2.>>
\ldots
Девятый: <<Это число больше 9.>>
Десятый: <<Это число больше 10.>>
Одиннадцатый: <<Это число меньше 10.>>
\ldots
Двадцатый: <<Это число меньше 1.>>
Сколько раз ребята сказали правду?
Условие
Трое детей решили две задачи, после чего каждый из них сделал два заявления об ответах, которые у них получились в этих задачах:
Первый: <<В первой задаче ответ больше 18. Во второй --- не больше 14.>>
Второй: <<В первой получается меньше 20, а во второй --- 14.>>
Третий: <<В первой ответ --- 15, а во второй ответ больше 14.>>
Известно, что один из них оба раза ошибся, а два других оба раза были правы. Какие ответы в этих задачах, если известно, что это --- целые числа?
Условие
Четверо друзей измеряли длину удава в попугаях. Получилось, что в удаве помещается целое число попугаев. Через неделю они стали вспоминать, какое же это число. Удав сказал: <<Меньше 50>>. Слоненок сказал: <<Меньше 45>>. Мартышка сказала: <<Меньше 44>>. А попугай сказал: <<Меньше 43>>. Известно, что ровно двое из них ошиблись. Какова длина удава?
Условие
На контрольной три школьника решали три задачи. Позже выяснилось, что каждый из них либо все три задачи решил верно, либо во всех трех ошибся. После урока дети обсудили, какие у них получились ответы.
Первый сказал: <<В первой задаче ответ больше 18. Во второй --- меньше 10. В третьей задаче ответ --- 20.>>
Второй сказал: <<В первой получается меньше 18, а во второй --- 10. В третьей получается больше 20.>>
Третий сказал: <<В первой ответ --- 18, а во второй ответ больше 10. В третьей ответ меньше 20.>>
Сколько из них решили все задачи верно?
Условие
Встретились четыре артиста А, Б, В и Г. Каждый из них через раз говорит правду, а через раз --- ложь. Между ними произошёл следующий разговор:
А: Б --- клоун.
Б: В --- клоун.
В: А --- клоун.
В: Б --- клоун.
Б: Г --- клоун.
А: Я сам клоун.
Сколько из этих артистов являются клоунами?
Условие
Жители города Правдин всегда говорят правду, а жители города Лгунов всегда лгут. В одном из городов состоялся футбольный матч между командами этих городов. После матча около стадиона на остановке автобуса, идущего в другой город, произошел следующий диалог:
А: Я не был на матче. Скажите, кто выиграл?
Б: Г сказал мне, что их команда проиграла.
В: Наша команда выиграла.
Г (садясь в автобус): Поедем вместе, А, ведь мы из одного города.
А: Вы ошибаетесь Г, Я живу здесь. Это В из Вашего города.
Определите, кто из какого города, и где происходил футбольный матч.
А из города __, Б из города __, В из города __, Г из города __, матч был в городе __.
Условие
Три мальчика разговаривают после урока:
Антон: Я получил за контрольную 5!
Борис: Я написал работу не хуже, чем Вадим.
Вадим: Антон написал контрольную на 4.
Антон: Кстати, Борис написал её на 4.
Борис: Вадим получил 4.
Вадим: Я получил 5.
Известно, что один мальчик оба раза солгал, а остальные сказали правду. Определите, кто из них написал контрольную работу на 4.
Условие
В семейном ансамбле <<Ласковый лай>> участвуют Тит Фомич, Фома Титович, Фома Фролович, Фрол Фомич и Фрол Фролович Собакины. Один из них поет, его отец играет на шарманке, брат держит микрофон, а дети бьют в барабан. Назовите имя и отчество певца.
Условие
Четверо друзей --- Коля, Саша, Олег и Антон --- соревновались в поедании конфет. После окончания соревнований каждого из них спросили, какое он место занял. Ребята дали следующие ответы:
Коля: <<Я не был ни первым, ни последним.>>
Саша: <<Я не был первым.>>
Олег: <<Я был первым.>>
Антон: <<Я был последним.>>
Оказалось, что трое мальчиков сказали правду, а один соврал. Выясните, кто победил в этом соревновании.
Условие
Известно, что разведчик, перевербованный контрразведкой, всегда лжет. Нормальный же разведчик всегда говорит чистую правду. На конспиративной квартире встретились два разведчика. Между ними произошел следующий разговор:
А: Мы с Вами встречались в Берне.
В: Я никогда там не был !!?
А: Разберемся позже. Вот дипломат с бомбой.
Посмотрев в дипломат, В сказал:
В: Да, это действительно бомба.
После этого они разошлись. А что говорит каждый из них --- правду или ложь?
А говорит __, В говорит __.
Условие
Среди приведённых высказываний найдите такие утверждения А и Б, что из А следует Б.
В ответ запишите пары пунктов высказываний без пробела. Если ответов несколько, запишите их все через пробел.
Например,
вг аб
(Для въедливых: мы считаем истиной, что существует хотя бы одно какое-нибудь число.)
а) Все числа чётные,
б) Все числа нечётные,
в) Пять - чётное число,
г) Существуют нечётные числа.