\justifying \large
\begin{frame} { аттестация10 }
При каких натуральных значениях а корни уравнения 9x^2-2x-a^2 = 0 рациональны?
\end{frame}\begin{frame} { аттестация09 }
Среди первых ста членов арифметической прогрессии с положительной разностью есть три числа 13/6, 75/2 и 389/6. Найдите d - разность этой прогрессии и наименьшее из возможных значений первого члена прогрессии a.
В ответе укажите отношение a/d виде неправильной несократимой дроби.
\end{frame}\begin{frame} { аттестация08 }
Какое наименьшее число ладей нужно поставить на доску 9×9 так, что если снять все ладьи, стоящие на белых полях, то оставшиеся ладьи будут бить все белые поля, а если снять все ладьи, стоящие на чёрных полях, то оставшиеся ладьи будут бить все чёрные поля?
\end{frame}\begin{frame} { аттестация08 }

\begin{frame} { аттестация07 }

\begin{frame} { аттестация07 }
_Памятка
1. На острове живут аборигены двух племён: рыцари, которые обладают способностью всегда говорить правду, лжецы, которые обладают способностью всегда говорить ложь, если они (лжецы или рыцари) не находятся под воздействием магов.
2. Среди аборигенов обоих племён встречаются маги, обладающие даром менять способности простых аборигенов на противоположные: если в компании присутствует маг, то обязательно в компании найдётся простой абориген (и только один), находящийся под его воздействием (на всё время его нахождения в этой компании).
3. Маги не могут действовать на одного и того же аборигена одновременно.
4. Маги не могут действовать друг на друга, а действуют только на обычных аборигенов.
5. На острове могут (в разных компаниях по-разному) встречаться шесть видов аборигенов: рыцари маги (обозначение МР), лжецы маги (МЛ), рыцари, находящиеся под воздействием магов (Р*), лжецы, находящиеся под воздействием магов (Л*), просто рыцари, которые не маги и не находятся под воздействием магов (Р), и просто лжецы, которые не маги и не находятся под воздействием магов (Л)._
Девять аборигенов (см. памятку выше) стоят по кругу. Среди них ровно три мага. Каждый сказал, что среди его соседей нет магов. Найти наибольшее возможное число лжецов (любого вида) среди них.
\end{frame}\begin{frame} { аттестация06 }
На каждой клетке доски 5×5 лежит по одинаковой монете. Среди них есть ровно четыре фальшивых, которые одинакового веса и легче настоящих. ОлЮр знает, что фальшивые монеты лежат по диагонали (см. рис.).
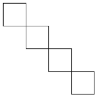
За какое наименьшее число взвешиваний на чашечных весах без гирь ОлЮр сможет найти четыре настоящих монеты?
\end{frame}\begin{frame} { аттестация06 }
На одну доску записали 25 натуральных чисел, а на другую – НОД всех пар чисел первой доски. Оказалось, что каждое число, встречающееся на одной доске, встречается и на другой. Какое наибольшее количество различных чисел могло быть на первой доске?
\end{frame}\begin{frame} { аттестация05 }
На каждой клетке доски 5×5 лежит по одинаковой монете. Среди них есть ровно четыре фальшивых, которые одинакового веса и легче настоящих. ОлЮр знает, что фальшивые монеты лежат по диагонали (см. рис.).

За какое наименьшее число взвешиваний на чашечных весах без гирь ОлЮр сможет найти все фальшивые монеты, если на каждую чашку весов можно класть только по одной монете?
\end{frame}\begin{frame} { аттестация05 }
В полном графе на 2025 вершинах каждое ребро покрасили либо в красный, либо в синий цвет. Что можно сказать о двух получившихся графах – красном и синем? В каждом из двух графов по 2025 вершин.
\end{frame}\begin{frame} { аттестация04 }
В прямоугольнике 3×8 стоят 24 аборигена (см. памятку). Присутствуют все 6 видов. Каждый сказал: «У меня все четыре соседа – маги».
Сколько магов (любого вида) может быть?
Соседними считаются клетки, имеющие общую сторону.
\end{frame}\begin{frame} { аттестация04 }
В графе 20 вершин. Степень каждой равна 8. Какое наибольшее количество вершин можно выбрать так, чтобы между выбранными вершинами не было ни одного ребра?
\end{frame}\begin{frame} { аттестация03 }
В квадрате 3×3 стоят 9 аборигенов (см. памятку). Каждый сказал:
«У меня ровно четыре соседа – маги».
Какое наибольшее число магов-рыцарей может быть? Соседними считаются клетки, имеющие общую сторону.
\end{frame}\begin{frame} { аттестация03 }
Для семизначного числа разрешается выполнять такое его изменение: выбрать любые две соседние цифры, ни одна из которых не равна нуля, вычесть из них по 1 и поменять эти цифры местами. Какое самое маленькое число можно получить из числа 3456789 с помощью таких операций?
\end{frame}\begin{frame} { аттестация02 }
Дано простое число p. Сколько решений в натуральных числах уравнение, если слева в нем сумма двух простейших дробей со знаменателями a и b, а справа аналогичная дробь со знаменателем p?
\end{frame}\begin{frame} { аттестация02 }

\end{frame}
\begin{frame} { аттестация01 }

\begin{frame} { аттестация01 }
Сумма двух двузначных чисел равна 74. А чему может быть равна сумма этих же чисел, записанных в обратном порядке? В ответ укажите сумму возможных значений.
\end{frame}\begin{frame} { аттестация00 }
Укажите фамилии и имена участников вашей группы через пробел запятую
\end{frame}\begin{frame} { арифметикаНЧ28 }
Во сколько раз число $2023\cdot2022\cdot2021\cdot...\cdot2\cdot1$ больше числа $2022\cdot2021\cdot2020\cdot...\cdot2\cdot1$. Кстати, первое из них называется 2023 факториал, а второе – 2022 факториал.
\end{frame}\begin{frame} { арифметикаНЧ27 }
На сколько число 2023·2022·2021 больше числа 2024·2022·2020?
\end{frame}\begin{frame} { арифметикаНЧ26 }
На сколько число 1111111·6666667 меньше чем 2222222·3333334?
\end{frame}\begin{frame} { арифметикаНЧ25 }
На сколько число $1001\times 1005$ меньше числа $1002\times 1004$?
\end{frame}\begin{frame} { арифметикаНЧ24 }
На сколько число $1001\times1003$ меньше числа $1002\times1002$?
\end{frame}\begin{frame} { арифметикаНЧ23 } Если к числу прибавить 10% от него, а потом у полученного числа вычесть 10%, то сколько процентов от исходного числа получится? \end{frame}
\begin{frame} { арифметикаНЧ22 }
На сколько число $1001\times1002$ меньше числа $1002\times1003$?
\end{frame}\begin{frame} { арифметикаНЧ21 }
Чему равна сумма цифр числа 999999999999·2023? В первом множителе двенадцать девяток.
\end{frame}\begin{frame} { арифметикаНЧ20 }
На сколько число $102\cdot201$ больше числа $101\cdot 202$?
\end{frame}\begin{frame} { арифметикаНЧ19 }
Вычислите в уме 10·9-9·8+8·7-7·6+6·5-5·4+4·3-3·2
\end{frame}\begin{frame} { арифметикаНЧ18 }
На сколько число $101\cdot200$ больше числа $100\cdot 201$? А можно это понять не вычисляя произведения?
\end{frame}