Выберите серию
Ослица и мул шли вместе, нагруженные мешками равного веса. Ослица жаловалась на тяжесть ноши. «Чего ты жалуешься, — сказал мул, — если ты мне дашь один твой мешок, моя ноша станет вдвое больше твоей, а если я дам тебе один мешок, наши грузы только сравняются». Сколько мешков было у каждого?
У ослицы __ мешков, у мула __.





Ответ:
Варианты ответов:
Пусть у ослицы было О мешков, а у мула - М мешков. Если ослица даст мулу один мешок, то у неё останется О-1 мешок, а у мула - М+1 мешок. По условию М+1=2(О-1), то есть $М=2О-3. Если же мыл даст ослице мешок, то у ослицы будет О+1 мешок, а у мула М-1, и по условию О+1=М-1, то есть М=О+2. Отсюда М=О+2=2О-3, 2+3=2О-О$, $О=5$, $М=7$. Итак, у ослицы пять мешков, а у мула семь.
У мальчика в два раза больше братьев, чем сестер, а у его сестры втрое меньше сестер, чем братьев. Сколько в этой семье мальчиков и сколько девочек?
Мальчиков __, девочек __.





Ответ:
Варианты ответов:
Пусть в семье $m$ мальчиков и $d$ девочек. Тогда у мальчика $m-1$ брат и $d$ сестёр, и по условию, $m-1=2d$, то есть $m=2d+1$. А у его сестры $m$ братьев и $d-1$ сестра, и по условию $m=3(d-1)$. Отсюда $2d+1=3d-3$, то есть $1+3=3d-2d$, $d=4$. Тогда $m=9$.
Ведро, полное воды, весит 15 килограмм. То же ведро, но заполненное водой наполовину, весит столько же, сколько и два пустых ведра. А сколько весит пустое ведро?





Ответ:
Варианты ответов:
Пусть $x$ - вес пустого ведра, а $15-x$ - вес воды в нём. Тогда $x+\frac{15-x}{2}=2x$, то есть $\frac{15-x}{2}=x$, $15-x=2x$, $3x=15$, $x=5$. Итак, ведро весит 5 кг.
Фигура на картинке составлена из квадратов. Чему равна
сторона нижнего левого квадрата, если сторона самого маленького
квадратика равна 1?
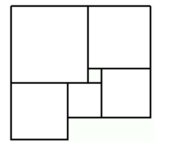





Ответ:
Варианты ответов:
Обохначим за $x$ сторону квадрата, который находится строго ниже единичного квадратика (этот квадрат - самый маленький из оставшихся). Тогда сторона квадрата в правом нижнем углу равна $x+1$, в правом верхнем углу - $x+2$, в левом верхнем - $x+3$. Тогда сторона искомого квадрата равна $x+4-x=4$.
Заяц набрал мешок яблок. По пути домой он половину мешка отдал медведю, а треть оставшегося - козе. После этого он отдал ежу половину того, что у него осталось. Напоследок он отдал все, кроме одного яблока, кроту. Оказалось, что медведю досталось на 75 яблок больше, чем кроту. Сколько яблок досталось козе?





Ответ:
Варианты ответов:
Пусть у зайца было $x$ яблок. Тогда медведю досталось $x/2$ яблок, козе - $x/6$ (после козы у зайца осталось $x/3$ яблок). Ежу досталось $x/6$, кроту - $x/6-1$. Отсюда $x/2=x/6-1+75$, то есть $x/3=76$, откуда $x/6=38$. Итак, козе досталось 38 яблок.