Даны 4 множества, по 28 элементов в каждом. Любые два пересекаются по 21 элементу, любые три – по 15, а в пересечении всех четырёх – 10 элементов. Сколько элементов в объединении?

Как известно, есть 28 человек, решивших последнюю задачу.

Теперь посчитаем количество остальных. Для остальных верно, что среди них каждую задачу из первых трёх решило $28-21=7$ человек, потому что каждую задачу решило 28 человек, из которых 21 решил ещё и последнюю. Любые две задачи решило $21-15=6$ из них, так как из 21 человека, решившего данные две задачи, 15 решило ещё и последнюю. А все три задачи решило $15-10=5$ человек.

Временно забыв про 28 человек, решивших последнюю задачу, можно считать, что в контрольной было 3 задачи, каждую из которых решило 7 человек, любые 2 – 6 человек, а все 3 – 5 человек. Первую и вторую решили те, кто решил только первую и вторую, и те, кто решил все три задачи. Последних – 5 человек, поэтому только первую и вторую задачи решил ровно 1 участник.

Аналогично только вторую и третью решил 1 человек, и только первую и третью – тоже 1 человек. Из людей, решивших первую, 5 решило и вторую и третью, 1 решил ещё только вторую, и 1 решил ещё только 3. Всего их 7, значит не людей, решивших только первую задачу.

Аналогично, понимаем, что нет людей решивших ровно одну задачу. Тогда всего их $5+1+1+1=8$.

Теперь вспомним про забытых 28 человек, и получим, что всего участников, которые хоть что-то решили $8+28=36$.

Контрольная состояла из 4 задач, каждую решило по 28 человек. При этом для любых двух задач нашелся ровно 21 человек, решивший обе. Для любых трёх задач ровно 15 людей решило их все. Сколько всего людей решило хоть что-то, если известно, что 10 человек решили все 4 задачи?

Даны множества $A$, $B$ и $C$. Известно, что $|A|=|B|=|C|=15$, $|A\cap B|=7$, $|B\cap C|=6$, $|C\cap A|=9$ и $|A\cup B\cup C|=28$. Найдите $|A\cap B\cap C|$.

Чтобы найти количество людей, выучивших все три стихотворения, вычтем из количества людей, выучивших первое и второе, количество тех, кто выучил только первое и второе. Для этого нужно найти количество школьников, выучивших только первое и второе стихотворения. Тех, кто не выучил третье стихотворение – $28-25=13$ человек. Из них $15-9=6$ выучили первое, $15-6=9$ – выучили второе. Тогда тех из них, кто выучил только второе – $13-6=7$, значит оставшиеся 2 человека из выучивших второе – выучившие первые два стихотворения. Значит детей, выучивших все три стихотворения $7-2=5$.

Каждый из 28 учеников 7В класса , готовясь к уроку литературы, выучил хотя бы одно из трёх стихотворений. Оказалось, что каждое из стихотворений выучило по 15 ребят.

При этом и первое, и второе выучили 7 человек, второе и третье – 6 человек, а первое и третье – 9. Сколько детей выучили выучили все три стихотворения?

Даны множества $A$, $B$ и $C$. Известно, что $|A|=|B|=|C|=15$, $|A\cap B|=4$, $|B\cap C|=5$, $|A\cap B\cap C|3$ и $|A\cup B\cup C|=29$. Найдите $|A\cap C|$

Дети, выучившие первое и третье стихотворения, это трое ребят, выучившие все три стихотворения, и те, кто выучил первое и третье, но не выучил второе. Посчитаем их количество. Рассмотрим детей не выучивших 2 стихотворение. Всего их $29-15=14$. Из них $15-4=11$ выучили первое, а $15-5=10$ --- третье, и каждый выучил хоть что-то. Нужно найти количество тех из них, кто выучил и первое и третье. Из этих 14 детей 10 выучили третье, значит оставшиеся 4 --- только первое. Тогда из тех, кто выучил первое, 4 выучили только первое, значит остальные 7 выучили и третье. То есть среди не выучивших второе 7 детей выучили первое и третье. Итого детей выучивших первое и третье стихотворения $3+7=10$ человек.

Каждый из 29 учеников 7Б класса , готовясь к уроку литературы, выучил хотя бы одно из трёх стихотворений. Оказалось, что каждое из стихотворений выучило по 15 ребят. При этом и первое, и второе выучили 4 человека, а второе и третье --- 5 человек. Сколько детей выучили и первое, и третье стихотворение, если известно, что трое выучили все три?

0

0

*Условие.*

_Каждый из 29 учеников 7Б класса , готовясь к уроку литературы, выучил хотя бы одно из трёх стихотворений. Оказалось, что каждое из стихотворений выучило по 15 ребят. При этом и первое, и второе выучили 4 человека, а второе и третье --- 5 человек. Сколько детей выучили и первое, и третье стихотворение, если известно, что трое выучили все три?_

*Решение.*

Дети, выучившие первое и третье стихотворения, это трое ребят, выучившие все три стихотворения, и те, кто выучил первое и третье, но не выучил второе. Посчитаем их количество. Рассмотрим детей не выучивших второе стихотворение.

Всего их $29-15=14$.

Из них __ выучили первое, а __ – третье, и каждый выучил хоть что-то.

Нужно найти количество тех из них, кто выучил и первое и третье. Из этих 14 детей 10 выучили третье, значит оставшиеся 4 – только первое.

Тогда из тех, кто выучил первое, __ выучили только первое, значит остальные 7 выучили и третье. То есть среди не выучивших второе 7 детей выучили первое и третье.

Итого детей выучивших первое и третье стихотворения $3+7=10$ человек.

Даны множества $A$, $B$ и $C$. Известно, что $|A|=|B|=15$, $|A\cap B|=7$, $|B\cap C|=4$, $|C\cap A|=3$, $|A\cap B\cap C|=2$ и $|A\cup B\cup C|=30$. Найдите $|C|$

Дети, выучившие третье стихотворение бывают 4 типов: 1)Выучившие все три стихотворения. Таких по условию 2. 2)Выучившие только первое и третье стихотворение. Чтобы их посчитать, вычтем из количества детей, выучивших первое и третье, число тех из них, кто выучил ещё и второе, и получим $3-2=1$ ребенок. 3)Выучившие только второе и третье стихотворение. Чтобы их посчитать, вычтем из количества детей, выучивших второе и третье, число тех из них, кто выучил ещё и первое, и получим $4-2=2$ ребенка 4)Выучившие только третье стихотворение. Чтобы посчитать их количество, посчитаем количество остальных, и вычтем из общего числа. Остальные --- это те, кто выучил хотя бы одно из первых двух стихотворений. Тех кто выучил первое --- 15, а тех, кто выучил второе, но не первое --- $15-7=8$. Суммарно таких детей 23. Значит тех, кто выучил только третье --- $30-23=7$. Последним действием, сложим все найденные количества, чтобы получить общее число выучивших третье стихотворение. $2+1+2+7=12$ детей.

Каждый из учеников 7А класса, готовясь к уроку литературы, выучил хотя бы одно из трёх стихотворений. Оказалось, что каждое из первых двух стихотворений выучило по 15 ребят, при этом и первое, и второе выучили 7 человек. И первое, и третье стихотворение выучили трое, а второе и третье – четверо. Сколько детей выучили третье стихотворение, если известно, что двое выучили все три?

0

0

Заполните пропуски в решении задачи.

*Условие.*

_Каждый из 30 учеников 7А класса, готовясь к уроку литературы, выучил хотя бы одно из трёх стихотворений. Оказалось, что каждое из первых двух стихотворений выучило по 15 ребят, при этом и первое, и второе выучили 7 человек. И первое, и третье стихотворение выучили трое, а второе и третье – четверо. Сколько детей выучили третье стихотворение, если известно, что двое выучили все три?_

*Решение.*

Дети, выучившие третье стихотворение бывают 4 типов:
1) Выучившие все три стихотворения. Таких по условию 2.
2) Выучившие только первое и третье стихотворение. Чтобы их посчитать, вычтем из количества детей, выучивших первое и третье, число тех из них, кто выучил ещё и второе, и получим $3-2=1$ ребенок.
3) Выучившие только второе и третье стихотворение. Чтобы их посчитать, вычтем из количества детей, выучивших второе и третье, число тех из них, кто выучил ещё и первое, и получим __ ребенка
4) Выучившие только третье стихотворение. Чтобы посчитать их количество, посчитаем количество остальных, и вычтем из общего числа.

Остальные – это те, кто выучил: 
a) хотя бы одно из первых двух стихотворений;
б) первое и второе стихотворения;
в) только первое или только второе.
Ваш вариант ответа: __ 

Тех кто выучил первое – 15, а тех, кто выучил второе, но не первое – $15-7=8$. Суммарно таких детей 23.

Значит тех, кто выучил только третье – __.

Последним действием, сложим все найденные количества, чтобы получить общее число выучивших третье стихотворение. $2+1+2+7=12$ детей.

Даны множества $A$, $B$ и $C$. Известно, что $|A|=|B|=12$, $|A\cap B|=7$, $|B\cap C|=6$, $|C\cap A|=9$ и $|A\cap B\cap C|=5$. Найдите $|(A\cup B)\backslash C|$

Посчитаем общее количество детей, записавшихся на плавание или волейбол. 12 детей записались на плавание. Ещё 12 записались на волейбол, но 7 из них записаны на плавание. Значит, всего детей, записанных на плавание или волейбол: $12+(12-7)=17$. Из этих 17 детей некоторые записались и на борьбу. Посчитаем их количество. Есть 9 детей записавшихся на борьбу и на плавание. И ещё 6 на борьбу и волейбол, но 5 из этих 6 записаны и на плавание. Итого, детей записанных на борьбу и на что-нибудь из плавания и волейбола: $9+(6-1)=10$. Требуется посчитать количество детей, записавшихся на что-то из плавания и волейбола, но не записавшихся на борьбу. Для этого достаточно вычесть из количества людей, записавшихся на что-то из плавания и волейбола (таких, как было посчитано --- 17), количество тех из них, кто записан ещё и на борьбу (таких, как было посчитано --- 10). Тогда искомое количество равно $17-10=7$.

Одноклассники записывались в спортивные секции: по плаванию, волейболу и борьбе. Известно, что на секции по плавнию и волейболу записалось по 12 человек, при этом пятеро записалось на все три секции. Семеро записалось и на плавание, и на волейбол, 6 – и на волейбол, и на борьбу, а 9 – и на плавание, и на борьбу.

Найдите количество детей, не записавшихся на борьбу, если каждый куда-то записался.

Даны множества $A$, $B$ и $C$. Известно, что $|A|=|B|=|C|=15$, $|A\cap B|=4$, $|B\cap C|=5$, $|C\cap A|=11$ и $|A\cap B\cap C|=3$. Найдите $|A\cup B\cup C|$.

Дети, изучающие языки, делятся на 7 типов по набору изучаемых ими языков. Детей, изучающих все три языка, по условие трое. Чтобы посчитать количество детей, изучающих ровно два конкретных языка, например, английский и французский, надо из общего числа детей, изучающих английский и французский вычесть количество детей, изучающих ещё и немецкий. То есть детей, изучающих только английский и французский --- $4-3=1$. Аналогично, $5-3=2$ ребёнка изучают только французский и немецкий, и $11-3=8$ детей --- только английский и немецкий. Чтобы посчитать количество детей, изучающих ровно один конкретный язык, например, английский, надо из общего числа детей, изучающих английский, вычесть количество детей, изучающих что-то ещё. Есть три варианта, что ещё кроме английского дети могут учить. Либо они, в добавок к английскому, учат и французский и немецкий --- таких 3 ребёнка. Либо учат ещё французский, но не немецкий, таких, как мы посчитали ранее --- 1 ребёнок. Либо учат ещё немецкий, но не французский. А таких, как было посчитано ранее --- 7 человек. Итого только английский учат $15-3-1-8=3$. Аналогично, только французский учат $15-3-1-2=9$ детей, а только немецкий --- $15-3-2-8=2$ ребёнка. Осталось сложить все найденные количества, чтобы узнать общее число детей. $3+1+2+8+3+9+2=28$ детей учат языки.

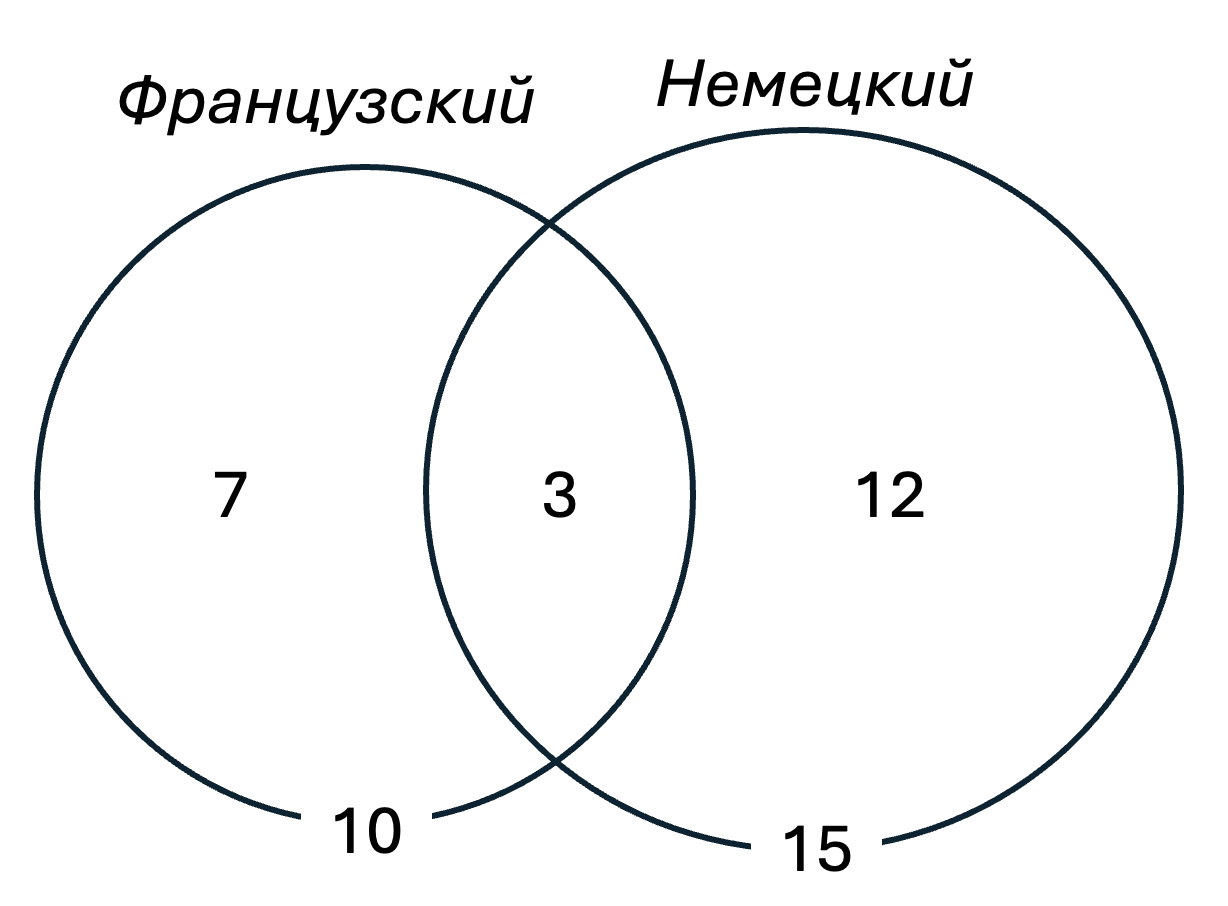
Ученики класса изучают иностранные языки: английский, французский и немецкий. Каждый язык учит 15 человек. При этом и английский, и французский изучают 4 человека, французский и немецкий ---5 детей, а английский и немецкий --- 10. Сколько всего детей изучает языки, если есть ровно 3 ребёнка, изучающих все три языка?

0

Заполните пропуски в решении задачи.

*Условие.*

_Ученики класса изучают иностранные языки: английский, французский и немецкий. Каждый язык учит 15 человек. При этом и английский, и французский изучают 4 человека, французский и немецкий – 5 детей, а английский и немецкий – 10. Сколько всего детей изучает языки, если есть ровно 3 ребёнка, изучающих все три языка?_

*Решение.*

Дети, изучающие языки, делятся на __ типов по набору изучаемых ими языков.
Детей, изучающих все три языка, по условие трое. Чтобы посчитать количество детей, изучающих ровно два конкретных языка, например, английский и французский, надо из общего числа детей, изучающих английский и французский вычесть количество детей, изучающих ещё и немецкий. То есть детей, изучающих только английский и французский – $4-3=1$.
Аналогично, __ ребёнка изучают только французский и немецкий, и 8 детей – только английский и немецкий. Чтобы посчитать количество детей, изучающих ровно один конкретный язык, например, английский, надо из общего числа детей, изучающих английский, вычесть количество детей, изучающих что-то ещё.
Есть __ варианта, что ещё кроме английского дети могут учить.

Либо они, в добавок к английскому, учат и французский и немецкий – таких 3 ребёнка.
Либо учат ещё французский, но не немецкий, таких, как мы посчитали ранее --- 1 ребёнок.
Либо учат ещё немецкий, но не французский. А таких, как было посчитано ранее --- 7 человек.

Итого только английский учат $15-3-1-8=3$.

Аналогично, только французский учат __ детей, а только немецкий – 2 ребёнка. Осталось сложить все найденные количества, чтобы узнать общее число детей. $3+1+2+8+3+9+2=28$ детей учат языки.

Даны множества $A$, $B$ и $C$. Известно, что $|A|=14$, $|A\cap B|=10$, $|A\cap C|=5$ и $|A\cap B\cap C|=4$. Найдите $|A\backslash (B\cup C)|$.

Чтобы посчитать число детей, увлекающихся только рисованием, нужно вычесть из общего числа детей, увлекающихся рисованием, число тех, кто занимается ещё чем-то другим. Если ребенок занимается не только рисованием, то для него есть 3 варианта.
1) Он увлекается и музыкой и танцами. Таких по условию четверо.
2) Он увлекается музыкой, но не увлекается танцами.
3) Он увлекается танцами, но не музыкой.

Посчитаем количество детей второго типа. Всего детей увлекающихся музыкой и рисованием 10, из них надо вычесть число тех, кто занимается ещё и танцами, а таких четверо. Итого детей, кто увлекается рисованием и музыкой, но не танцами, всего $10-4=6$.

Аналогично, посчитаем число детей третьего типа. Всего детей увлекающихся танцами и рисованием – 5, из них надо вычесть число тех, кто занимается ещё и танцами, а таких четверо. Итого детей, кто увлекается рисованием и музыкой, но не танцами, всего $5-4=1$ ребёнок.

Итого, из детей, увлекающихся рисованием, чем-то ещё другим занимаются $4+6+1=11$ человек. Значит, оставшиеся 3 ребёнка увлекаются только рисованием.

Некоторые из учеников увлекаются рисованием, музыкой и танцами. При этом известно, что 14 ребят увлекается рисованием, 10 – рисованием и музыкой, 5 – рисованием и танцами, а 4 интересуется и рисованием, и музыкой, и танцами. Сколько детей увлекается только рисованием?

Даны множества $A$, $B$ и $C$. Известно, что $|A|=10$, $|B|=10$, $|C|=10$, $|A\cap B|=3$, $|B\cap C|=2$, $|C\cap A|=1$ и $|A\cap B\cap C|=0$. Найдите $|A\cup B\cup C|$

Дети, посещающие кружки, делятся на 6 типов, по тому, какие кружки они посещают.

Есть 3 типа детей, посещающих ровно два кружка:
1) это дети, занимающиеся математикой и физикой;
2) дети, занимающиеся математикой и информатикой,
3) и дети, занимающиеся физикой и информатикой.

Из условия таких суммарно $2+3+1=6$ человек.

Ещё есть три типа детей, посещающих только один кружок:

1) те, кто ходят только на математику;
2) те, кто ходят только на физику;
3) те, кто ходят только на информатику.

Посчитаем количества детей этих типов отдельно. Чтобы узнать, сколько детей занимаются только математикой, надо вычесть из общего количества детей занимающихся математикой, количество тех детей, кто занимается не только математикой. А именно количество тех, кто занимается ещё и физикой, и тех, кто занимается ещё и информатикой. Значит, детей занимающихся только математикой – $10-2-3=5$.

Теперь посчитаем число детей, занимающихся только физикой. Из 10 детей, занимающихся физикой $2+1=3$ занимаются ещё чем-то.

Значит, занимающихся только физикой – $10-3=7$. Аналогично, детей занимающихся только информатикой – $10-3-1=6$.

Чтобы найти общее число детей, сложим количества детей каждого из типов. Итого получается $2+3+1+5+7+6=24$

Для учеников класса работают кружки по математике, физике и информатике, в каждом занимается по 10 человек. При этом, у кружков по физике и математике 2 общих участника, у кружков по математике и информатике – 3 общих, а у кружков по физике и информатике – только 1 общий участник.

Сколько всего детей посещает кружки, если нет ребенка, занимающегося во всех трёх кружках?

Даны три множества $A, B, C$. Известно, что $|A|=4$, $|B|=15$, $|C|=10$, $|A\cap B|=2$, $|B\cap C|=5$, $|A\cap C|=0$. Найдите $|A\cup B\cup C|$

Детей, получивших четверку, по условию 15 человек. Все остальные получили либо только пятёрку, либо только тройку, либо ничего. Посчитаем количество детей, получивших только тройку. Всего детей получивших тройку – 10, никто из них не получил пятёрки, а 5 – получили четверку. Тогда детей получивших только тройку – $10-5=5$. Теперь посчитаем количество детей, получивших только пятёрку. Всего детей получивших пятёрку – 4, никто из них не получил тройки, а 2 – получили четверку. Тогда детей получивших только тройку – $4-2=2$. Итого получается $15+5+2=22$ ребёнка.

За один учебный день некоторые из учеников получили тройки, четверки и пятерки. При этом оказалось, что пятерки получили 4 человека, четверки – 15, а тройки – 10. Известно что и пятерку, и четверку получило двое детей, а и четверку, и тройку – пятеро, но никто не получил и пятёрку, и тройку одновременно. Сколько всего детей получивших оценки?

Даны множества $A$ и $B$. Известно, что $|A|=24$, $|B|=15$, $|A\cup B|=30$. Найти $|A\cap B|$.

Всего в классе $30-24=6$ детей, пропустивших линейку в 1 классе. Из условия мы знаем, что они были на линейке во второй год. Во второй год на линейке было 15 детей, 6 из них не были в предыдущем году, значит остальные 9 – были.

Из 30 учеников второго класса каждый хотя бы раз был на линейке 1 сентября. При этом 24 ребёнка были на линейке в первом классе, и 15 детей – во втором. Сколько ребят присутствовали на линейке оба раза?

...

Заполните пропуски в решении задачи.

*Условие.*

_Из 30 учеников второго класса каждый хотя бы раз был на линейке 1 сентября. При этом 24 ребёнка были на линейке в первом классе, и 15 детей – во втором. Сколько ребят присутствовали на линейке оба раза?_

*Решение.*

Всего в классе $30-24=6$ детей, пропустивших линейку в 1 классе. Из условия мы знаем, что они __ 1) были 2) не были на линейке во второй год.

Во второй год на линейке было 15 детей, __ из них не были в предыдущем году,
значит остальные __ – были.

Даны подмножества $A$ и $B$ в множестве $C$. Известно, что $|C|=32$, $|A|=10$, $|B|=16$, $|A\cap B|=7$. Найти $|C\backslash (A\cup B)|$.

Всех детей можно разделить на 4 группы.

1) Дети, получившие и четверку, и пятёрку. Таких по условию 7.
2) Дети, получившие четверку, но не пятёрку.
3) Дети, получившие пятёрку, но не четверку.
4) Дети, не получившие ни того, ни другого.

Заметим, что дети, получившие четвёрку, это в точности дети из групп 1 и 2. Значит детей во второй группе $16-7=9$.

Дети, получившие пятёрку, это дети из групп 1 и 3. Тогда детей в группе 3 – $10-7=3$.

Теперь, зная количества детей во всех группах кроме четвертой, и общее количество, посчитаем число детей в группе 4. Их $32-7-9-3=13$.

Из класса, в котором учится 32 человека, за день некоторые дети получили оценки (возможно несколько). Пятёрку получило 10 человек, а четверку – 16. Сколько детей не получило ни четверки, ни пятёрки, если семеро получили и четверку и пятёрку?

Даны множества $A$ и $B$. Известно, что $|A|=26$, $|A\cup B|= 30$, $|A\cap B|= 10$. Найти $|B|$.

Дети, которым понравилась вторая книга, это дети, которым понравились обе книги, и дети, которым понравилась только вторая. Первых – 10 человек, как мы знаем из условия. Вторые, это в точности те, кому не понравилась первая книга, поскольку нет детей, которым ничего не понравилось. Известно, что из 30 детей 26 полюбили первую книгу, значит тех, кому она не понравилась, – $30-26=4$. Итого, детей, которым понравилась вторая книга $10+4=14$.

Ученики за каникулы прочитали две книги. Первая книга понравилась 26 детям, а обе книги – десяти. Скольким детям понравилась вторая книга, если оказалось, что каждому из всех   30 учеников класса понравилось хоть что-то из прочитанного?

Даны множества $A$ и $B$. Известно, что $|A|=14$, $|B|=6$, $|A\cap B|=4$. Найти $|A\cup B|$.

Из детей, присутствовавших на занятии хотя бы раз, 14 были во вторник. Тогда остальные – это в точности дети, пришедшие в четверг, но не пришедшие во вторник. В четверг на занятии было 6 человек, из которых 4 было и во вторник. Значит детей, присутствоваших только в четверг --- $6-4=2$. Итого всего детей, пришедших хотя бы раз --- $14+2=16$.

В классе некоторые из учеников записались на занятия по танцам, проходящие по вторникам и четвергам. Известно, что во вторник занятие посетили 14 человек, в четверг – 6. При этом четверо были на занятии оба раза.

Сколько детей хотя бы раз присутствовали на занятиях?

Даны множества $A$ и $B$. Известно, что $|A|=14$, $|B|=6$, $|A\cap B|=4$. Найти $|A\cup B|$.

Из детей, присутствовавших на занятии хотя бы раз, 14 были во вторник. Тогда остальные – это в точности дети, пришедшие в четверг, но не пришедшие во вторник. В четверг на занятии было 6 человек, из которых 4 было и во вторник. Значит детей, присутствоваших только в четверг – $6-4=2$. Итого всего детей, пришедших хотя бы раз – $14+2=16$.

Заполните пропуски в решении задачи.

*Условие.*

_В классе некоторые из учеников записались на занятия по танцам, проходящие по вторникам и четвергам. Известно, что во вторник занятие посетили 14 человек, в четверг – 6. При этом четверо были на занятии оба раза.

Сколько детей хотя бы раз присутствовали на занятиях?_

*Решение.*

Из детей, присутствовавших на занятии хотя бы раз, 14 были во вторник. Тогда остальные – это в точности дети, пришедшие в четверг, но не пришедшие во вторник. В четверг на занятии было 6 человек, из которых __ было и во вторник.

Значит детей, присутствоваших только в четверг – двое. Итого всего детей, пришедших хотя бы раз – __ + __ = __.

Даны множества $A$ и $B$. Известно, что $|A|=20$, $|B|=16$, $|B\backslash A|=7$.

Найти $|A\backslash B|$.

Из условия знаем, что из 16 детей, занимающихся географией, 7 не занимаются историей. Значит оставшиеся $16-7=9$ занимаются. Тогда и наоборот, из 20 детей, занимающихся историей, 9 изучают и географию. Тогда остальные 11 детей, изучающих историю, учат только историю.

В классе 20 человек дополнительно занимаются историей, а 16 – географией. Сколько человек занимаются историей, но не географией, если известно, что 7 детей изучают географию, но не историю.

Даны множества $A$ и $B$. Известно, что $|A|=20$, $|B|=16$, $|B\backslash A|=7$. Найти $|A\backslash B|$.

Из условия знаем, что из 16 детей, занимающихся географией, *7* не занимаются историей. Значит оставшиеся $16-7=9$ занимаются и тем, и другим.

Тогда и наоборот, из 20 детей, занимающихся историей, *11* изучают и географию.

Тогда остальные *19* детей, изучающих историю, учат только историю.

Заполните пропуски в решении задачи.

*Условие.*

_В классе 20 человек дополнительно занимаются историей, а 16 – географией. Сколько человек занимаются историей, но не географией, если известно, что 7 детей изучают географию, но не историю?_

*Решение.*

Из условия знаем, что из 16 детей, занимающихся географией, __ не занимаются историей. Значит оставшиеся $16-7=9$ занимаются и тем, и другимпори.

Тогда и наоборот, из 20 детей, занимающихся историей, __ изучают и географию.

Тогда остальные __ детей, изучающих историю, учат только историю.

порисовав имеет смысл добиться осознанного понимания какие именно части множеств даны и как что легче искать 

Даны множества $A$ и $B$. Известно, что $|A|=10$, $|B|=15$, $|A\cap B|=3$. Найти $|(B\backslash A)\cup(A\backslash B)|$.

Дети, которые учат только 1 языка делятся на 2 типа:
те, которые учат только французский,
и те, которые учат только немецкий.

Посчитаем количества детей этих типов по отдельности. Всего детей занимающихся немецким – 15. Они делятся на два типа:
изучающие оба языка,
и изучающие только немецкий.

Первых по условие трое. Тогда дети, изучающие только немецкий – это оставшиеся 12 человек. Аналогично, всего детей, изучающих французский – 10, и из них 3 изучают оба языка.

Значит, только французским занимаются оставшиеся 7 детей. Итого один язык изучают 19 человек.

Из учеников одного класса 10 человек изучают французский язык, а 15 – немецкий. При этом оказалось, что трое из них учат оба языка. Сколько детей учат только один язык?

Даны множества $A$ и $B$. Известно, что $|A|=10$, $|B|=15$, $|A\cap B|=3$.

Найти $|(B\backslash A)\cup(A\backslash B)|$.

Заполните пропуски в решении предыдущей задачи *множества05*.

Дети, которые учат только 1 языка делятся на 2 типа:
а) те, которые учат только французский;
б) те, которые учат только немецкий.

Посчитаем количества детей этих типов по отдельности.

Всего детей занимающихся немецким – 15. Они делятся на два типа:
1) изучающие оба языка,
2) изучающие только немецкий.

Первых по условие трое. Тогда дети, изучающие только немецкий – это оставшиеся __ человек.

Аналогично, всего детей, изучающих французский – 10, и из них 3 изучают оба языка. Значит, только французским занимаются оставшиеся __ детей.

Итого один язык изучают __ человек.

Даны множества $A$ и $B$. Известно, что $|A\backslash B|=8$, $|B\backslash A|=10$, $|A\cup B|=20$. Найти $|A\cap B|$.

Все дети, посещающие музыкальную школу, делятся на 3 типа: те, кто учится играть только на скрипке; те, кто учится играть только на фортепиано; и те, кто занимается на обоих инстурментах. Всего их – 20, детей первого типа – 8, второго – 10, значит к третьему типу относятся оставшиеся $20-8-10=2$ ребёнка.

20 человек из класса занимаются в музыкальной школе, и там учатся играть на скрипке или фортепиано. 8 из них учатся только игре на скрипке, а 10 – только игре на фортепиано. Сколько детей изучает оба инструмента?

Даны множества $A$ и $B$. Известно, что $|A|=10$, $|B|=15$, $|A\cap B|=3$. Найти $|B\backslash A|$.

Всего детей занимающихся немецким – 15. Они делятся на два типа: изучающие оба языка, и изучающие только немецкий. Первых по условие трое. Тогда дети, изучающие только немецкий – это оставшиеся $15-3=12$ человек.

Из учеников одного класса 10 человек изучают французский язык, а 15 – немецкий. При этом оказалось, что трое из них учат оба языка.

Сколько детей занимаются только немецким?

Следует обратить внимание на корректность при указании количеств во множествах, если рисуются Круги Эйлера:

Даны множества $A\subset B$, известно, что $|B|=20$, $|A|=13$, найти $|B\backslash A|$.

Из 20 человек 13 посещают дополнительные занятия. Те, кто не посещает занятий, это оставшиеся $20-13=7$ человек.

В классе 20 человек и 13 из них ходят на дополнительные занятия по русскому языку. Сколько учеников не посещают дополнительных занятий?

В множестве элементов выбраны два подмножества.

В скольки подмножествах может содержаться фиксированный элемент?

Всех учеников можно разделить на 4 типа.

1) Не посещают никаких кружков.
2) Посещают только кружок по математике.
3) Посещают только кружок по физике.
4) Посещают оба кружка.

Если ученик относится к первому типу, то он занимается в 0 кружков, если ко второму или третьему – то 1 кружок, а если к последнему – 2 кружка.

Для учеников класса, в котором учится Ренат, проводят кружки по математике и по физике.

Какое количество кружков может посещать Ренат?

Можно порисовать на  кругах Эйлера, и после обсуждения помочь выделить три случая : посещает 0 кружков, посещает 1 (либо М, либо Ф), и посещает оба -- и М, и Ф.