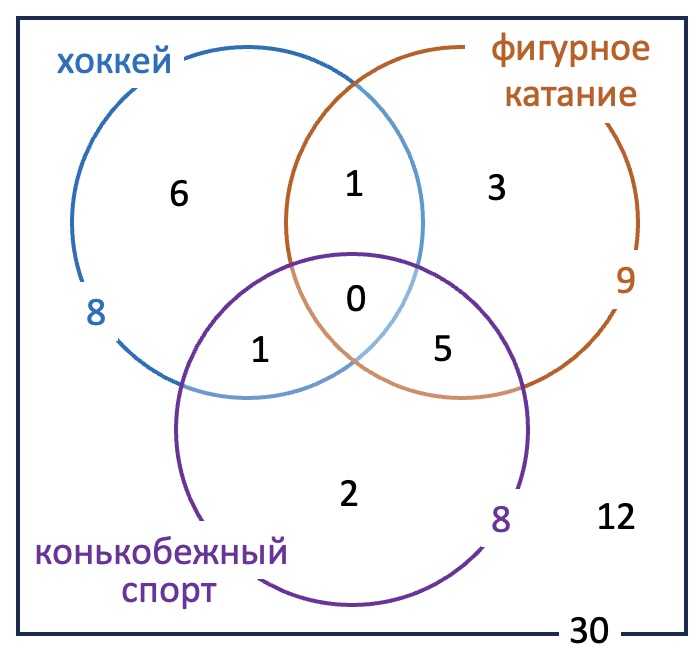
В одном из классов интересной спортшколы учится 30 ребят. Из них хоккеем занимаются 8, фигурным катанием – 9, 8 – конькобежным спортом (из которых двое – только им). Ровно один ученик ходит на тренировки и по фигурному катанию, и по хоккею одновременно, но он не любит конькобежный спорт. Пятеро – одновременно на фигурном катании и конькобежном спорте. Все остальные всё время уделяют ходьбе. Сколько существует вариантов отправить на соревнования команду из спортсмена, который занимается хотя бы двумя видами спорта, и любителя ходьбы?

Из условия следует, что тремя видами спорта не занимается никто. Двое занимаются только конькобежным спортом, пятеро - конькобежным спортом и фигурным катанием. Всего занимаются конькобежным спортом восемь человек, а сосчитано из них $2+5=7$. Значит, один человек занимается конькобежным спортом и хоккеем. Получается, что семеро занимаются двумя видами спорта. Только хоккеем занимаются $7-1-1=5$, только фигурным катанием: $9-5-1=3$. Тогда хотя бы одним из видов спорта занимаются $5+3+2+1+1+6=18$ детей. Остальные 12 занимаются ходьбой. Составить пару спортсмена, удовлетворяющих условию задачи, можно $7 \cdot 12 = 84$ способами.

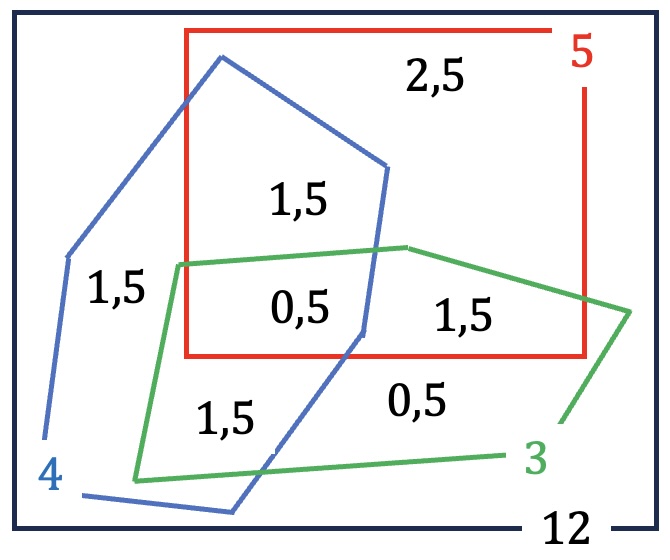
На полу размером 3 × 4 м лежат три ковра. Площадь одного ковра 5 кв. м, другого - 4 кв. м, третьего - 3 кв. м. Каждые два ковра перекрываются на площади 1,5 кв. м. Все три ковра перекрываются на площади 0,5 кв. м. Найдите площадь не покрытой части пола. В ответе укажите число, выразив площадь в кв. м.

Площадь комнаты - 12 кв.м. Если каждые два ковра перекрываются на площади 1,5 кв.м., то площадь пересечения любых двух ковров, не накрытая третьим ковром, равна 1 кв.м. Тогда площадь, покрытая только первым ковром, равна 5-1-1-0,5=2,5 кв.м, только вторым - 4-1-1-0,5=1,5 кв.м., только третьим - 3-1-1-0,5=0,5 кв.м. Общая покрытая площадь равна 0,5+1+1+1+2,5+1,5+0,5=8 кв.м. Значит, непокрытой оказалось 4 кв.м.

В классе каждый ученик занимается спортом, музыкой или языками. Спортом занимается 15 детей, музыкой - 13, языками - 12 детей. Семеро занимаются спортом и музыкой, шестеро - спортом и языками, пятеро - музыкой и языками. А какое наибольшее количество человек могло быть в классе?

Обозначим за $x$ количество учеников, которые занимаются всеми тремя видами деятельности. Тогда только спортом и музыкой занимаются $7-x$ человек, только спортом и языками - $6-x$, только музыкой и языками - $5-x$. Тогда только спортом занимается $2+x$ учеников, только музыкой - $1+x$, только языками - тоже $1+x$. Складывая эти все числа, получаем $x+22$ учеников. Так как x не может быть больше $5$ (потому что $5-x$ занимаются музыкой и языками), получаем, что наибольшее количество учеников - $27$.

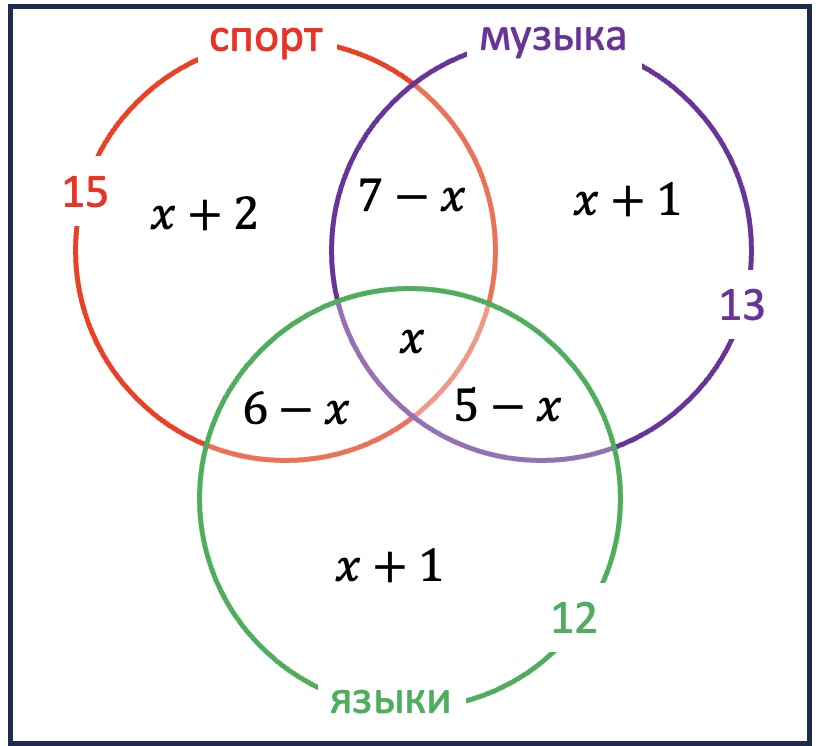
В первом решении, обозначив через неизвестное одно из подмножеств на схеме, удалось выразить количество детей в каждом из остальных подмножеств. Такой исследовательский подход помогает выразить все зависимости через одну переменную.

В этой задаче можно обойтись и без переменных, что удаётся не всегда. На примере этой задачи можно познакомить детей с идей формулы "включений-исключений".

Оценка.

Оценим возможно количество детей к классе. Если сложить количество спортменов, музыкантов и тех, кто изучает языки, то получим $15+13+12=40$ детей, но некоторые из них посчитаны более одного раза. А именно 7, которые занимаются спортом и музыкой, 6 - спортом и языками, 5 - музыкой и языками. Итак, $40-(7+6+5)=22$ ребенка, почти все из которых посчитаны по одном разу.

Но сколько раз мы посчитали тех, кто занимается и спортом, и музыкой, и языками? 

Сначала таких ребят мы включили трижды, а затем их исключили. Значит, их нужно снова включить. Итак, чем больше таких детей, тем больше и учащихся в классе. Но какое наибольшее количество детей могут такими активными? 

На самом деле их не более 5, так как именно столько занимаются музыкой и языками. Если все эти ещё и спортсмены, то как раз получается 5 активистов.

Значит, в классе не более 27 детей. 

Пример. Причём их может быть 27, если все три кружка посещают 5 детей.

Развитие задачи

Какое наименьшее количество учеников может быть в классе?

В классе каждый ученик занимается спортом, музыкой или языками. Спортом занимается 15 детей, музыкой - 13, языками - 12 детей. Семеро занимаются спортом и музыкой, шестеро - спортом и языками, пятеро - музыкой и языками. Какое наименьшее количество человек могло быть в классе?

Обозначим за x количество учеников, которые занимаются всеми тремя видами деятельности. Тогда только спортом и музыкой занимаются 7-x человек, только спортом и языками - 6-x, только музыкой и языками - 5-x. Тогда только спортом занимается 2+x учеников, только музыкой - 1+x, только языками - тоже 1+x. Складывая эти все числа, получаем x+22 ученика. Так как x не может быть отрицательным, наименьшее количество учеников окажется при x=0, т.е. 22.

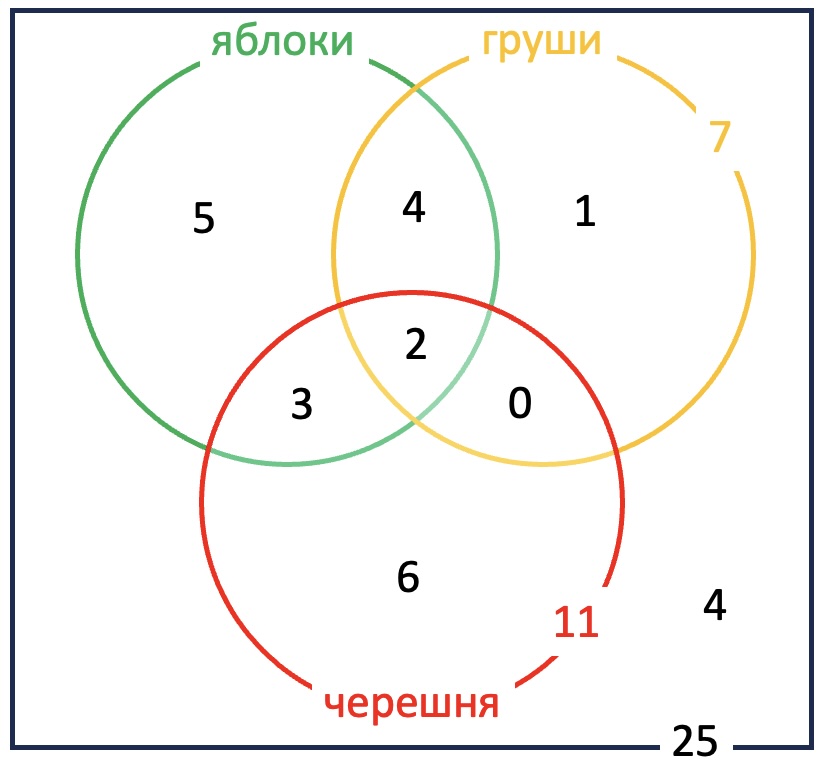
В одном классе 25 учеников. Из них 7 любят груши, 11 - черешню. Двое любят груши и черешню; 6 - груши и яблоки; 5 - яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фрукты вообще. Сколько учеников этого класса любят яблоки?

Двое любят все три вида фруктов. Значит, только груши и черешню любят 0 учеников, только груши и яблоки - 4, только черешню и яблоки - трое. Только груши любит один (7-4-2-0) человек, только черешню - 11-3-2-0=6 человек. Всего в классе 25 человек, четверо не любят никакие фрукты, 1+6+4+2+3=16 человек уже сосчитано, а не сосчитаны только те люди, которые любят только яблоки. Их получается 25-4-16=5. Тогда всего любителей яблок 5+4+3+2=14.

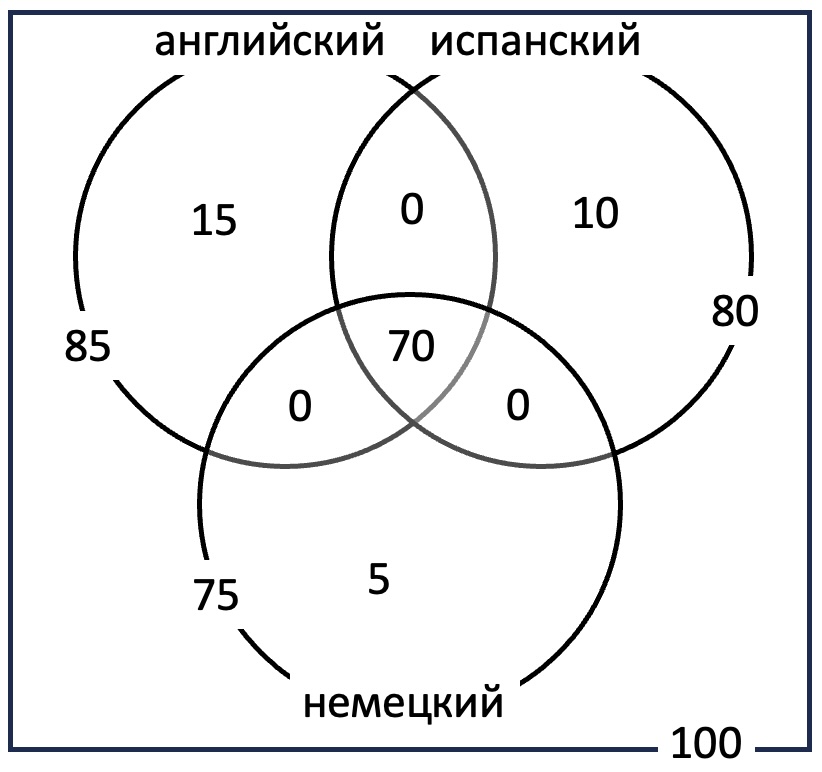
Из 100 человек 85 знают английский язык, 80 - испанский, 75 - немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

Если сложить количество людей, знающих английский, испанский и немецкий, получится 140. Но в этой сумме сосчитаны дважды люди, знающие два языка (таких нет по условию задачи) и трижды - знающие три языка. Значит, 240-100=140 - это дважды сосчитанные люди, владеющие всеми тремя языками. Отсюда людей, владеющих тремя языками, всего 70.

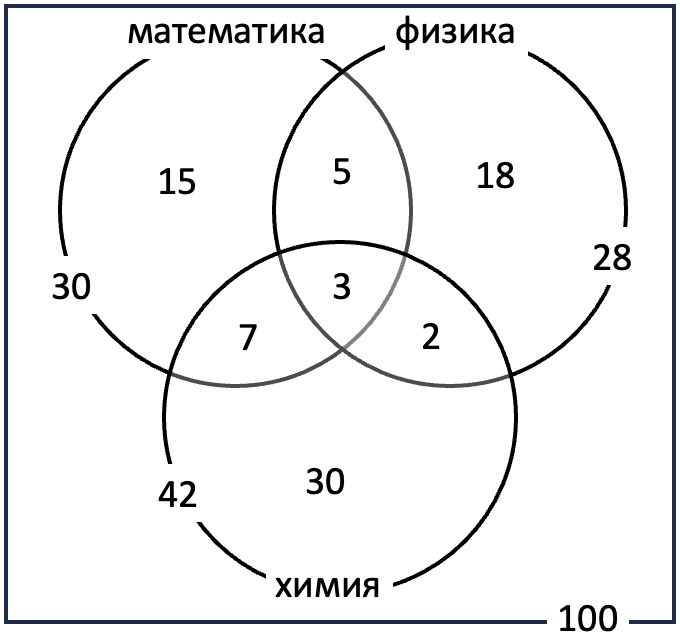
Из 100 ребят, отправляющихся в многопредметную школу, занимаются математикой 30 ребят, физикой — 28, химией — 42. Математикой и физикой занимаются 8 ребят, математикой и химией — 10, физикой и химией — 5, а всеми тремя предметами — 3. Ребята, которые не занимаются ни математикой, ни физикой, ни химией, являются биологами. Сколько биологов приехало в многопредметную школу?

Трое занимаются и математикой, и физикой, и химией. Значит, остальные 8-3=5 - только математикой и физикой, 5-3=2 - только физикой и химией, 10-3=7 - только математикой и химией. Тогда только математикой занимаются 30-7-5-3=15 школьников, только физикой - 28-5-2-3=18 школьников, только химией - 42-7-2-3=30 школьников. Значит, биологами являются 100-15-18-30-5-2-7-3=20 школьников.

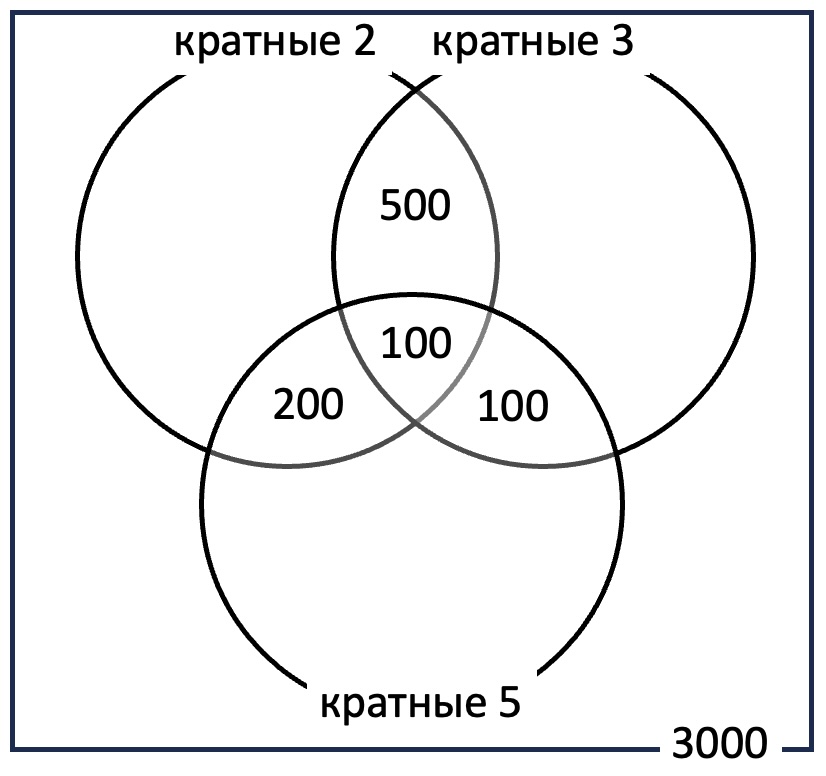
Сколько существует целых чисел от 1 до 3000, которые не делятся ни на 2, ни на 3, но делятся на 5?

Всего есть 600 чисел из данного диапазона, которые делятся на 5. Из них 300 чисел делятся на 2 (это числа, кратные 10), а 200 чисел - на 3. При этом 100 чисел входят в обе группы, т.к. делятся и на 2, и на 3, и на 5. Значит, ответ будет 600-300-200+100=200.

Здесь полезен приём "убери лишнее". Важно проверить, что лишнее убрали ровно 1 раз.

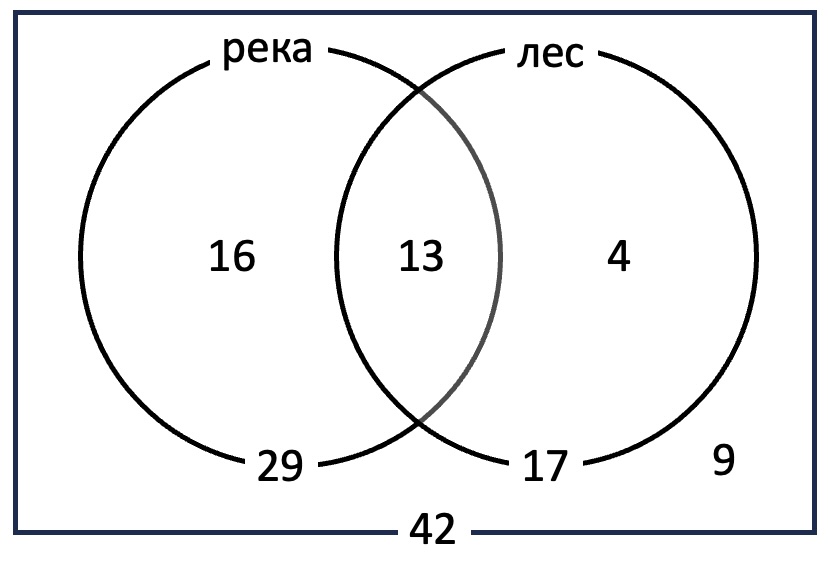
На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитали и Гарри Поттер, и Рон. Не нашлось ни одной книги, которую бы читал и Рон, и Гермиона. Гермиона прочитала 7 книг, которые не читал Гарри Поттер, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг.

Сколько книг прочитал только Рон?

Гарри прочитал 11 книг, ещё 7 книг прочитала только Гермиона, а значит, остальные 26-11-7=8 книг - только Рон. А всего Рон прочитал 12 книг. Но ответ к задаче: 8.

Некоторые условия в задаче оказались лишними.

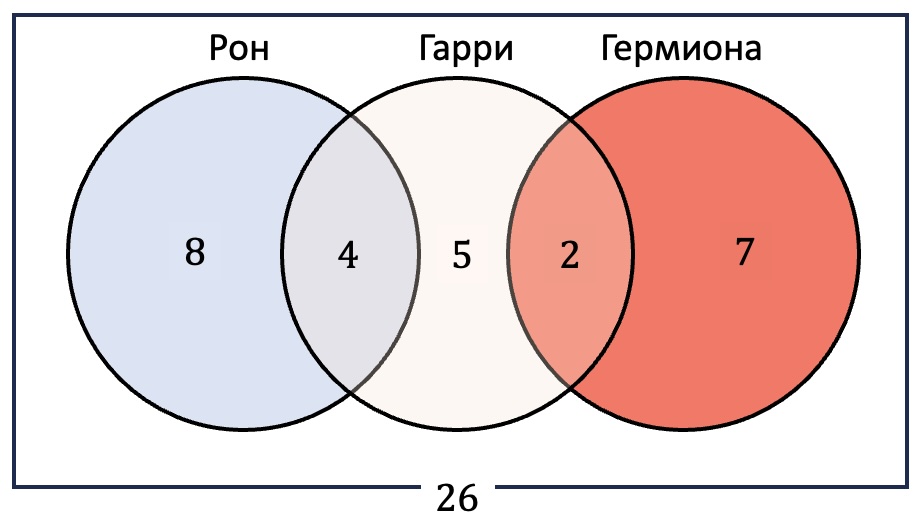
Известно, что в Майкопе каждый двадцатый пятиклассник пришел на Олимпиаду. А среди майкопских участников Олимпиады каждый пятнадцатый – пятиклассник. Кого в Майкопе больше: пятиклассников или участников олимпиады?

Обозначим за x количество пятиклассников, которые участвуют в олимпиаде. Тогда всего пятиклассников 20x, а участников олимпиады 15x. Ясно, что пятиклассников больше.

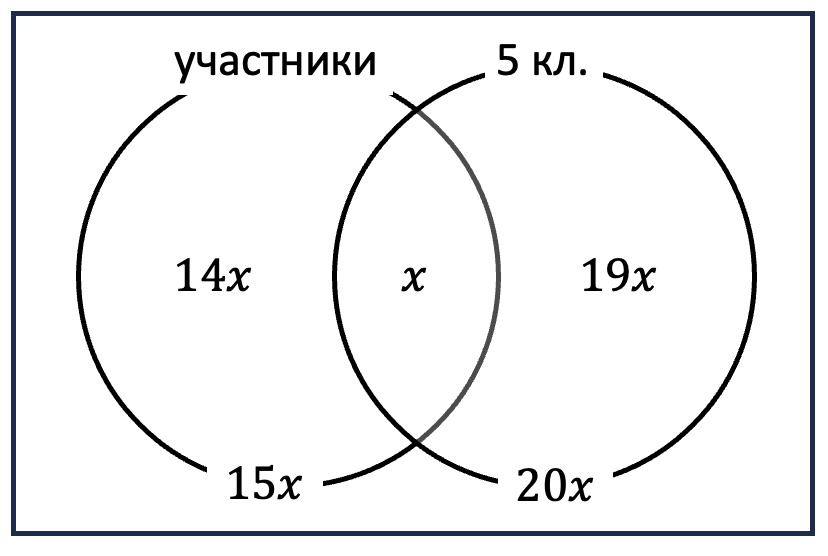
Сколько существует чисел от 1 до 60, которые не делятся ни на 2, ни на 3?

Среди чисел от 1 до 60 тридцать делятся на 2, 20 - на 3, а 10 - и на 2, и на 3. Значит, 10 чисел делятся на 3, но не на 2, а 30+10=40 чисел - на 2 или на 3. Оставшиеся 20 чисел не делятся ни на 2, ни на 3.

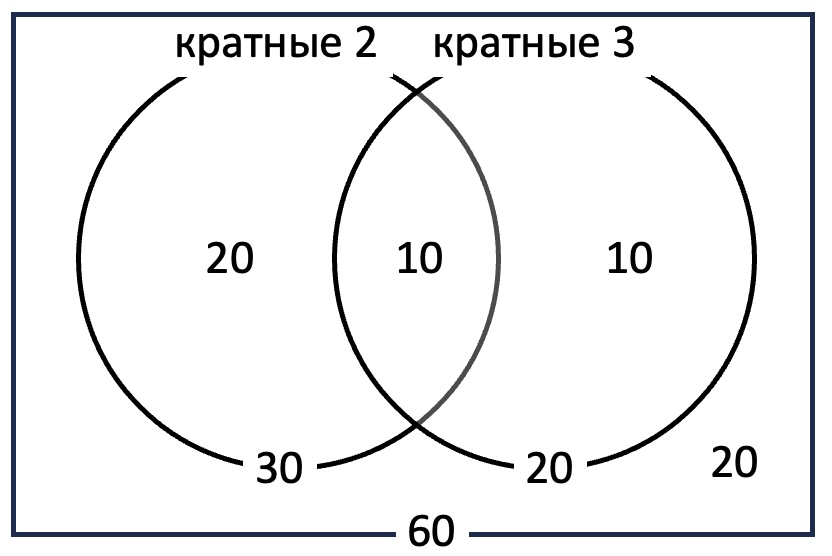
Художник Казимиров за месяц работы написал 42 картины. На 29 из них есть река, на 17 – лес, а на 13 – и то, и другое; на остальных картинах – не пойми что. Сколько картин изображают не пойми что?

На 17 картинах есть лес. На 29-13=16 картинах есть река, но нет леса. Значит, лес или река есть на 17+16=33 картинах. На оставшихся 42-33=9 картинах - не пойми что.

На доске нарисованы два пересекающихся круга, в которых отмечено несколько точек. Внутри первого круга отмечено 40 точек, внутри второго 30 точек, а 20 точек оказались внутри обоих кругов одновременно. Сколько точек всего было отмечено?

Внутри только первого круга (т.е. внутри первого, но не второго) отмечено 20 точек, внутри только второго - 10 точек. Значит, всего отмечено 20+10+20=50 точек.

Оформление диаграмм Эйлера-Венна требует особой аккуратности. Есть условности, позволяющие избежать логических ошибок. Мы рекомендуем следующее:

1. Числовое значение в области соотвествует только той из областей, которая ограничена ближашими линиями к этому значению.
2. Если область является универсальным множеством, то её изображают как прямоугольную рамку.
3. Количество элементов в таком случае указывают на границе области, оставив в ней небольшой разрыв.
4. Для множества, состоящего из нескольких областей допустим подход из пункта 3, но можно указать число рядом с границей не разрывая её.
5. Очень полезно пользоваться штриховкой или цветом для наглядности при указании тех или иных областей диаграммы.

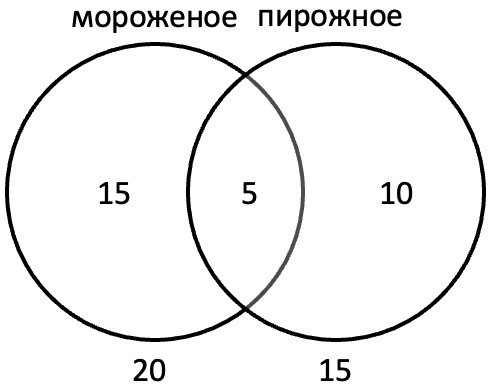
Тридцать детей пошли в кафе. Каждый из них выбрал мороженое, пирожное, или и то, и другое одновременно. Всего было продано 20 мороженых и 15 пирожных. Cколько детей ели только мороженое?

Если сложить количество сладостей, получим 35. Так как каждый из тридцати детей что-то себе покупал, то пятеро покупали и мороженое, и пирожное. А значит, только мороженое покупали себе 15 детей.

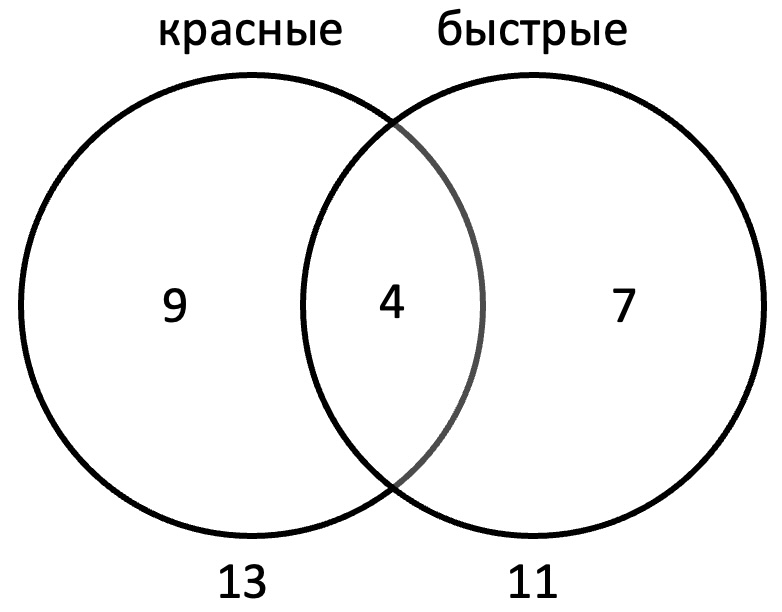
Каждая из 20 машинок - либо красная, либо быстрая, либо и красная, и быстрая. Красных машинок 13, быстрых - 11. Сколько машинок являются и красными, и быстрыми?

Если сложить количество красных и количество быстрых машинок, получится 24. Но всего машинок 20, а каждую красную быструю машинку сосчитали дважды. Следовательно, 4 машинки являются и красными, и быстрыми.