Выберите серию
Фигура на картинке составлена из квадратов. Чему равна
сторона нижнего левого квадрата, если сторона самого маленького
квадратика равна 1?
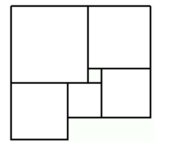





Ответ:
Варианты ответов:
Обохначим за $x$ сторону квадрата, который находится строго ниже единичного квадратика (этот квадрат - самый маленький из оставшихся). Тогда сторона квадрата в правом нижнем углу равна $x+1$, в правом верхнем углу - $x+2$, в левом верхнем - $x+3$. Тогда сторона искомого квадрата равна $x+4-x=4$.
Заяц набрал мешок яблок. По пути домой он половину мешка отдал медведю, а треть оставшегося - козе. После этого он отдал ежу половину того, что у него осталось. Напоследок он отдал все, кроме одного яблока, кроту. Оказалось, что медведю досталось на 75 яблок больше, чем кроту. Сколько яблок досталось козе?





Ответ:
Варианты ответов:
Пусть у зайца было $x$ яблок. Тогда медведю досталось $x/2$ яблок, козе - $x/6$ (после козы у зайца осталось $x/3$ яблок). Ежу досталось $x/6$, кроту - $x/6-1$. Отсюда $x/2=x/6-1+75$, то есть $x/3=76$, откуда $x/6=38$. Итак, козе досталось 38 яблок.
Иванов поступил на работу в Университет и стал писать по одной статье в год. Через пятнадцать лет он стал профессором и стал писать по две статьи в год. Ещё через некоторое время руководство Университета решило, что всем профессорам необходимо писать по 4 статьи в год. Иванов вздохнул и начал выполнять требование. А ещё через десять лет руководство Университета посчитало, что четырёх статей в год мало – нужно пять. Иванов проработал на таких условиях один год. После этого ему исполнилось 70 лет, и он ушёл на пенсию. За всё время работы он написал 90 статей. А во сколько лет он пришёл работать в Университет?





Ответ:
Варианты ответов:
Пусть Иванов писал по две статьи в год $x$ лет. Тогда он работал в Университете $15+x+10+1=26+x$ лет. И за это время он написал $15+2x+4\cdot 10+5\cdot 1=60+2x=90$ статей, откуда $2x=30$, $x=15$. Тогда он работал в Университете 41 год, а значит, пришёл в Университет в $70-41=29$ лет.
В одной школе ученики записывались на факультативные занятия.
На математику записались 60 человек, на лапту записались 50 человек, а на плетение фенечек - 40 человек. Перед началом учебного года составили три списка: тех, кто записался ровно на один факультатив; тех, кто записался ровно на два факультатива из трех; тех, кто записался на все три факультатива одновременно. Оказалось, что во всех списках одно и то же число человек. Сколько?





Ответ:
Варианты ответов:
Обозначим за $x$ искомое количество человек в каждом из списков. Посчитаем общее количество записей: $x$ человек записывались по одному разу, $x$ - по два раза (они создают $2x$ записей), и ещё $x$ - по три записи ($3x$ записей). Итого $x+2x+3x=6x$ записей.
С другой стороны, записей всего сделано 60+50+40=150. Итак, $6x=150$, откуда $x=25$.
В три коробки надо разложить 90 пакетов так, чтобы в первой коробке было вдвое больше пакетов, чем во второй, а во второй - на 2 пакета больше, чем в третьей. Сколько пакетов будет в первой коробке?





Ответ:
Варианты ответов:
Пусть $x$ - количество пакетов в первой коробке. Тогда во второй коробке - $x/2$ пакетов, а в третьей - $x/2-2$. Всего пакетов $x+x/2+x/2-2=2x-2=90$. Отсюда $2x=92$ и $x=46$.
Предприимчивый Георгий купил на рынке партию ручек и предлагает одноклассникам либо одну ручку за 5 рублей, либо три ручки за 10 рублей, потому что хочет от каждого покупателя получить одинаковую прибыль. А за сколько рублей Георгию в таком случае надо продавать ручки покупателю, который хочет купить 5 ручек?





Ответ:
Варианты ответов:
Пусть Р - стоимость одной ручки, а х - прибыль, которую Георгий хочет получить от каждого покупателя. Тогда Р+х=5, 3Р+х=10. Вычитая эти равенства, получим, что 2Р=5, откуда Р=2,5, х=2,5. Тогда 5Р+х=15.
Сумма семи последовательных чисел равна 210. Найдите самое маленькое из этих чисел.





Ответ:
Варианты ответов:
Пусть $x$, $x+1$, $x+2$, $x+3$, $x+4$, $x+5$ и $x+6$ - данные семь последовательных чисел. Складывая их, получим $7x+21=210$. Отсюда $7x=203$ и $x=29$.
За неделю до получения стипендии у четырех студентов осталось 45р. Если бы деньги первого студента увеличить на 2р., деньги второго уменьшить на 2р., деньги третьего увеличить вдвое, а деньги четвертого уменьшить вдвое, то у всех четверых денег было бы поровну. Сколько денег было у каждого студента?
У первого студента __ рублей, у второго __, у третьего __, у четвёртого __.





Ответ:
Варианты ответов:
Пусть $x$ - количество денег, которое было бы у каждого студента при выполнении указанных действий. Тогда сейчас у первого студента $x-2$ рубля, у второго $x+2$, у третьего $x/2$, у четвёртого $2x$, а всего $x-2+x+2+x/2+2x=45$, то есть $9x/2=45$, $x=10$. Тогда у первого студента было 8 рублей, у второго 12, у третьего 5, у четвёртого 20.
Маме 30 лет, дочке 3 года. Через сколько лет мама будет вдвое старше дочки?





Ответ:
Варианты ответов:
Обозначим искомую величину за $x$. Через $x$ лет маме будет $30+x$ лет, а дочке $x+3$ года. По условию, $x+30=2(x+3)$, откуда $30=x+6$, или $x=24$.
Васе на мороженое не хватает 10 рублей. Если Петя купит мороженое, то у него останется 30 рублей. Если Вася и Петя сложат свои деньги вместе, то они смогут купить ровно три мороженых. Сколько стоит одно мороженое?





Ответ:
Варианты ответов:
Пусть $x$ - цена мороженого. Тогда у Васи $x-10$ рублей, а у Пети $x+30$ рублей. Вместе у них $2x+20=3x$, так как они могут купить в точности три мороженых. Отсюда $x=20$.
В кабинете №1 было несколько человек, и они сильно шумели. За это половину из них выгнали в кабинет №2, но дети шумели и там. Тогда треть из тех, кто был в кабинете №2, снова перевели в кабинет №1, и там стало 16 человек. Сколько человек было изначально в кабинете №1?





Ответ:
Варианты ответов:
Пусть $x$ - количество детей в кабинете №1 изначально. После первого перевода в каждом кабинете будет по $x/2$ детей. Из второго кабинета вернули в первый $x/6$ детей, так что в первом кабинете осталось $2x/3$ детей. Итак, $2x/3=16$, $2x=48$, $x=24$.
Вера поставила на шахматную доску несколько фигур. Оказалось, что фигур поставлено в 7 раз меньше, чем свободных клеток на доске. Сколько фигур поставлено?





Ответ:
Варианты ответов:
Обозначим за $x$ количество поставленных фигур. Тогда $64-x=7x$ - количество свободных клеток. Отсюда $8x=64$ и $x=8$.
Я задумал число. Я отнял от него 2, умножил на 2, вычел задуманное число, прибавил 7, умножил на 2 и получил 40. Какое число я задумал?





Ответ:
Варианты ответов:
Обозначим за $x$ задуманное число. Проделав с ним указанные действия, получим выражение $((x-2)\cdot 2 - x + 7)\cdot 2 = 40$. Поделив обе части выражения на 2 и раскрыв скобки, получим $2x-4-x+7=20$, $x+3=20$, $x=17$.
На ферме живут коровы и куры. У них всех 50 голов и 170 ног. Сколько коров живёт на ферме?





Ответ:
Варианты ответов:
Обозначим количество коров за $x$, а количество кур за $50-x$. Тогда общее количество ног будет $4x+2(50-x)=2x+100=170$. Отсюда $2x=70$ и $x=35$.
Аня, Боря и Витя выполняли домашние задания. Аня решила на два примера больше Бори, а Витя – в два раза больше, чем Аня. В сумме ребята решили 30 примеров. Сколько из них сделала Аня?





Ответ:
Варианты ответов:
Обозначим за $x$ количество примеров, которые сделала Аня. Тогда Боря сделал $x-2$ примера, а Витя - $2x$ примеров. В сумме ребята решили $4x-2=30$ примеров. Тогда $4x=32$ и $x=8$. Значит, Аня решила 8 примеров.