В клетках квадрата 4x4 стоят островитяне. В некоторый момент каждый из них произнес: «Во всех соседних со мной по стороне клетках стоят лжецы». Какое наибольшее количество лжецов могло быть среди них?

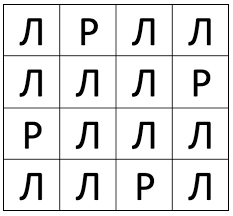
Заметим, что либо в углу, либо в клетке, соседней с угловой, должен стоять рыцарь (иначе лжец в углу будет говорить правду). Для разных углов такие клетки не пересекаются, а значит, рыцарей как минимум четверо. Пример четырёх рыцарей и 12 лжецов приведён на рисунке.

В течение одного вечера в дом заходили 20 жителей острова, и каждый из них (кроме первого) записал на специальном листе бумаги, кто вошел в дом перед ним — рыцарь или лжец. Если верить всем записям, то в дом входили только лжецы. Сколько на самом деле лжецов входили в этот дом?

Разобьём входящих на пары: первый со вторым, третий с четвёртым и т.д. В каждой паре стоят люди разных типов, иначе бы один из них назвал второго рыцарем. То есть в каждой паре ровно один лжец, а тогда лжецов десять.

Однажды каждый из 1000 островитян сказал: «Среди остальных 999 жителя острова есть по меньшей мере один лжец». Сколько рыцарей живет на острове?

Более одного лжеца быть не может - если есть хотя бы два лжеца, то каждый из них скажет правду. С другой стороны, все собравшиеся не могут быть рыцарями, иначе каждый из них солжёт. Значит, среди них 999 рыцарей.

В комнате находится пятеро островитян. Серёжа сказал Никите, а потом Вите: "Ты рыцарь." После этого он сказал Саше, а затем Паше: "Ты лжец!" Что скажет Паша про остальных?

Серёже: "Ты __"

Никите: "Ты __"

Вите: "Ты __"

Саше: "Ты __"

Фразу "Ты рыцарь" говорят друг другу островитяне одинакового типа, а фразу "Ты лжец" - разного. Следовательно, Серёжа, Никита и Витя одного типа, Саша и Паша другого. Значит, Паша первых троих назовёт лжецами, а Сашу рыцарем.

Путешественник, попавший на остров Рыцарей и Лжецов, встретил четырех людей и задал им вопрос: "Кто вы?". Известно, что среди них обязательно есть хотя бы один рыцарь и хотя бы один лжец. Он получил такие ответы: Первый: "Все мы лжецы". Второй: "Среди нас один лжец". Третий: "Среди нас два лжеца". Четвёртый: "Я ни разу не соврал и сейчас не вру". Кем является каждый из них? Если невозможно определить, кем является житель, напишите "неизвестно".

Первый: __

Второй: __

Третий: __

Четвёртый: __

Ясно, что первый солгал, а тогда среди них есть хотя бы один рыцарь. Первые три фразы противоречат каждая каждой, поэтому как минимум две из них ложные. Следовательно, среди островитян два или три лжеца.

Если лжецов двое, то это первый и второй (их фразы в этом случае ложные). Третий и четвёртый тогда рыцари, и этот вариант подходит.

Если лжецов трое, то первые три фразы ложные, а тогда четвёртый рыцарь. Такой вариант тоже подходит.

Три мальчика-островитянина разговаривают после урока:

Антон: Я получил за контрольную 5!

Борис: Я написал работу не хуже, чем Вадим.

Вадим: Антон написал контрольную на 4.

Антон: Кстати, Борис написал её на 4.

Борис: Вадим получил 4.

Вадим: Я получил 5.

Известно, что среди этих мальчиков ровно один лжец Определите, кто из них написал контрольную работу на 4.

Заметим, что первые фразы Антона и Вадима противоречат друг другу, а значит, хотя бы один из пары Антон - Вадим лжец. Также противоречат друг другу последние фразы Бориса и Вадима, а значит, один из них лжец. Так как лжец всего один, то это обязательно Вадим. Значит, Антон написал контрольную на 5, Борис на 4, Вадим на 4.

В комнате три островитянина. Первый сказал: «В комнате один рыцарь», второй ответил: «Нет, в комнате два рыцаря!», третий заявил: «В комнате все рыцари!». Сколько рыцарей может быть в комнате?

Поскольку все фразы противоречат друг другу, то в комнате максимум один рыцарь. Обе ситуации (когда все лжецы и когда первый является рыцарем) возможны.

Однажды в четверг после дождя между островитянами Тимом и Томом произошел следующий диалог:

– Ты можешь сказать, что я рыцарь, – гордо заявил Тим.

– Ты можешь сказать, что я лжец, – грустно ответил ему Том.

Кем являются Тим и Том?

Тим: __

Том: __

Оба рыцаря быть не могут, иначе никто не сможет произнести вторую фразу.

Если Тим рыцарь, а Том лжец, то Тим не сможет сказать свою фразу - ведь он знает, что Том говорит неправду и назовёт Тима лжецом.

Аналогично оба они не могут быть лжецами. В противном случае фраза Тима становится правдой - ведь Том лжец и назовёт Тима рыцарем.

Остаётся единственный вариант, и он подходит. В самом деле, Тим солгал, и Том не может назвать его рыцарем. А Том сказал правду: Тим лжец и назовёт Тома лжецом.

По кругу сидит 12 островитян. Каждый из них видит всех, за исключением своих соседей и, конечно, себя. Все люди по очереди сказали: <<Все, кого я вижу – лжецы>>. Сколько рыцарей сидит за столом?

Если есть хотя бы три рыцаря, то какие-то два из них не соседи, а тогда они видят друг друга и, значит, говорят неправду.

Если рыцарь всего один, то его сосед-лжец бкдет говорить правду.

Если рыцарей нет вовсе, то любой лжец скажет правду.

Два сидящих рядом рыцаря - единственная возможная ситуация.

За круглым столом сидят 7 островитян. Каждый из сидящих за столом сказал: <<Мои соседи – лжец и рыцарь>>. Определите, сколько среди них лжецов.

Пусть среди них есть рыцарь (назовём его А). Тогда его соседи - лжец и рыцарь (пусть Б). Вторым соседом Б должен быть лжец (пусть В). Чтобы В солгал, вторым его соседом должен быть рыцарь, и т.д. Получается цепочка ЛРРЛРРЛ, она замыкается (крайние лжецы сидят рядом), а тогда крайние лжецы скажут правду.

Собралась компания островитян разного роста. Каждый заявил «Среди тех, кто выше меня, есть лжецы». Сколько лжецов могло быть среди них?

Самый высокий из них, очевидно, лжец. А тогда каждый из остальных сказал правду.

Как-то раз встретились два островитянина и первый сказал второму: «По крайней мере один из нас – лжец». История умалчивает, ответил ли ему на это что-либо собеседник. Тем не менее определите, кем являются оба.

Первый: __

Второй: __

Сказавший не мог быть лжецом, иначе бы эта фраза оказалась правдой. Значит, первый должен быть рыцарем. Следовательно, среди островитян есть лжецы, а тогда второй лжец.

Встретились несколько островитян, и каждый заявил всем остальным: «Вы все — лжецы». Сколько рыцарей было среди них?

Более одного рыцаря быть не могло, иначе каждый из них скажет неправду. Но все быть лжецами тоже не могли, и наче каждый скажет правду.

Один из островитян сказал другому: «По крайней мере один из нас — рыцарь». «Ты — лжец», — ответил ему второй. Кто из них кто?

Первый: __

Второй: __

Допустим, первый лжец. Но тогда рыцарей среди них нет, но второй сказал правду, что невозможно. Значит, первый рыцарь, а тогда второй лжец.

Собрались двое островитян. Первый сказал: "По крайней мере один из нас лжец". Кто из них кто?

Первый __

Второй __

Первый рыцарь, иначе его фраза окажется правдой. Но если первый рыцарь, значит, один из этих двоих и правда лжец. Значит, лжецом является второй.

Собрались двое островитян. Первый сказал: "Мы оба лжецы". Кто из них кто?

Первый __

Второй __

Первый лжец, т.к. иначе фраза "Мы оба лжецы" оказалась заведомо ложной. Второй рыцарь, т.к. иначе та же фраза оказалась бы истинной.