В компании пять эльфов, пять гномов и один хоббит. У каждого эльфа по семь знакомых в этой компании, а у каждого гнома по два. Сколько знакомых в этой компании у хоббита?

Cложим количество знакомых у эльфов, гномов и хоббита. В этой сумме каждое знакомство мы сосчитали два раза (потому что в каждом знакомстве участвуют двое). Следовательно, эта сумма должна быть чётной, а потому количество знакомых у хоббита должно быть нечётным. Если их 7 и более, то присоединим хоббита к эльфам, тогда из этой группы должно выходить вовне не менее $6\cdot 2$ рёбер, а от гномов не более $5\cdot2$, и мы приходим к противоречию. Если знакомых у хоббита три и меньше, то присоединим хоббита к гномам. Тогда от эльфов должно исходить не менее $5\cdot3$ рёбер, а от гномов и хоббита не более $3+2\cdot5$, и мы снова приходим к противоречию.

В однокруговом турнире по настольному теннису каждый участник одержал четыре победы. Сколько человек участвовало в турнире?
Однокруговым называется турнир, в котором каждые двое игроков играют ровно одну партию. Ничьих в теннисе не бывает.

Первое решение. Пусть было всего $x$ игроков. Тогда партий всего было $x (x-1) / 2$ (каждый участвовал в x-1 партии, в каждой партии участвовало два игрока). С другой сороны, партий было столько же, сколько побед, а побед было 4x. Отсюда $x (x-1) / 2 = 4x$. Сократив на x и умножив выражение на 2, получим x-1=8, откуда x=9.

Второе решение. В каждой партии один человек выиграл, а один проиграл. Так как каждый участник выиграл 4 партии, то все остальные он проиграл. Заметим, что каждый сыграл одинаковое число игр (на один меньше, чем число людей), следовательно все проиграли тоже одинаковое число раз. Так как побед и поражений суммарно одинаково, то выходит, что у каждого ровно 4 поражения. Итого, у каждого 4 победы и 4 поражения. Значит, всего 8 игр, следовательно участников было 9.

Несколько человек пожимали друг другу руки, и оказалось, что каждый пожимал руки пятерым людям, а всего сделано 30 рукопожатий. А сколько людей в этом участвовало?

Пусть было x людей. Тогда было сделано 5 x / 2 рукопожатий (каждый пожимал руки пятерым, в каждом рукопожатии участвовали двое). Имеем 5 x / 2 = 30, откуда x=12.

Десять человек встретились, и некоторые стали пожимать друг другу руки. Оказалось, что трое пожали руки всем остальным людям, ещё двое – шестерым, ещё четверо - пятерым. Скольким людям мог пожать руки оставшийся человек:

а) одному;

б) двоим;

в) троим;

г) четверым?

Пусть x - количество рукопожатий последнего человека. Тогда всего рукопожатий было $(3\cdot9+2\cdot6+4\cdot5+x) / 2$. Так как это число должно быть целым, то х - нечётное. Но x не могло быть равно одному. Потому что трое пожимали руки всем остальным, а значит, каждый пожал руки хотя бы троим. Отсюда x=3.

Приведём пример, когда x=3. Трое пожали руки всем остальным; исключим их из рассмотрения. Оставшийся человек не мог больше никому пожать руку, поэтому исключим и его. Остались двое, которые пожимали руки троим (после вычета трёх рукопожатий у каждого) и ещё четверо, которые пожимали руки ещё двоим. Выстроим этих шестерых по кругу, и пусть каждый пожмёт руку своим соседям, а ещё двое противоположно расставленных людей пожмут руки друг другу. Получилась искомая конструкция.

Десять человек встретились, и некоторые стали пожимать друг другу руки. Оказалось, что трое пожали руки четырём людям, ещё двое - троим, ещё четверо - пятерым. Скольким людям пожал руки оставшийся человек:

а) одному;

б) троим;

в) четверым;

г) пятерым?

Пусть оставшийся человек совершил x рукопожатий. Сосчитаем, сколько всего было сделано рукопожатий. Это число равно $(3\cdot4+2\cdot3+4\cdot5+х) / 2$ (в каждом рукопожатии участвуют двое). Это число должно быть целым, откуда x должен быть чётным. А значит, оставшийся человек пожал руки четверым людям.

Вставьте пропущенные числа в решение задачи

***"Могут ли 13 шахматистов устроить такой турнир, чтобы каждый шахматист сыграл ровно пять партий?"***

Решение с пропусками:

– Так как каждый из шахматистов участвовал в пяти партиях, то все они садились за игру __ раз в совокупности.

– Но в каждой партии участвуют __ игрока, а значит, всего должно было пройти __ партий.

– Это число нецелое, поэтому такой ситуации быть не может.

Вставьте пропущенные числа в решение задачи

*Могут ли 13 шахматистов устроить такой турнир, чтобы каждый шахматист сыграл ровно пять партий?*

Решение с пропусками:

– Так как каждый из шахматистов участвовал в пяти партиях, то все они садились за игру __ раз в совокупности.

– Но в каждой партии участвуют __ игрока, а значит, всего должно было пройти __ партий.

– Это число нецелое, поэтому такой ситуации быть не может.

Игроки  - вершины графа

Число партий - степень вершин

Вершин нечетной степени четное число.

Десять человек встретились, и некоторые стали пожимать друг другу руки. Оказалось, что двое пожали руки четырём людям, ещё двое - троим, ещё четверо - пятерым, и оставшиеся двое пожали руки всем остальным людям. Сколько всего было рукопожатий?

Сосчитаем, сколько раз люди протягивали руки для рукопожатий. Это $2\cdot4+2\cdot 3+4\cdot5+2\cdot 9=52$. Но в каждом рукопожатии участвовали двое, поэтому рукопожатий в два раза меньше.

Каждый из десяти человек пожал руку остальным. Сколько было рукопожатий?

Решение 1. Каждый пожимал руку девяти людям, то есть все вместе пожимали руки 90 раз. Но в каждом рукопожатии участвуют двое, поэтому рукопожатий было в два раза меньше.

Решение 2. Посмотрим на первого человека. Он должен пожать руку девяти другим. Теперь рассмотрим второго человека. Он мы уже сосчитали его рукопожатие с первым, и теперь должны сосчитать ещё восемь рукопожатий с его участием. У следующего человека останется 7 неучтённых рукопожатий, и т.д. В итоге получим 9+8+7+6+5+4+3+2+1+0=45 рукопожатий.

Задача имеет  решения, которые использут разные подходы в подсчете.

1) Подсчет удвоенного числа рукопожатий (отрезок с двумя концами);

2) Следить за каждым человеком по очереди и заметить сумму последовательных чисел.

Новый год встречали Маша, мама, папа и бабушка. В полночь они налили в свои бокалы лимонад и стали чокаться. Каждый хотел чокнуться со всеми остальными (с каждым по разу). А в соседней комнате сидел обиженный попугай и считал, сколько раз звенели бокалы. Какое число у него получилось?

Решение 1. Назовём дзиньком каждый раз, когда двое чокались. Пусть Маша чокнулась со всеми (попугай сосчитал три дзинька). Мама должна чокнуться ещё с папой и бабушкой (два дзинька, потому что дзиньк мамы с Машей уже сосчитали). Ещё папа должен чокнуться с бабушкой - итого 6 дзиньков.

Решение 2. Каждый из четверых должен чокнуться три раза. Итого все вместе протягивали руки для чоканий 12 раз. Но в каждом чокании участвуют двое, поэтому всего было 6 чоканий.

В Солнечной системе планируется следующее межпланетное сообщение: от Меркурия будут рейсы до Венеры, Земли и Юпитера, от Венеры - до Меркурия, Земли и Сатурна, от Земли - до Меркурия, Венеры, Марса, Юпитера и Сатурна, от Марса - до Земли, Юпитера, Сатурна и Урана. Кроме того, Юпитер будет связан с Сатурном, Ураном и Нептуном. На каждый рейс потребуется один космический корабль. Сколько кораблей понадобится?

Сосчитаем все рейсы. Чтобы не считать рейсы дважды, будем считать только рейсы, направленные от внутренних планет к внешним. От Меркурия отходит 3 таких рейса, от Венеры – два не посчитанных (рейс до Меркурия мы уже сосчитали), от Земли – три не посчитанны, от Марса – три не посчитанны, от Юпитера тоже три. Итого 14 рейсов.

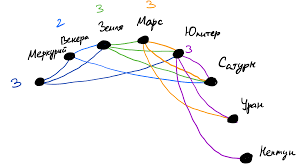
В Солнечной системе планируется следующее межпланетное сообщение:

– от Меркурия будут рейсы до Венеры, Земли и Юпитера,

– от Венеры - до Меркурия, Земли и Сатурна,

– от Земли - до Меркурия, Венеры, Марса, Юпитера и Сатурна,

– от Марса - до Земли, Юпитера, Сатурна и Урана.

Кроме того, Юпитер будет связан с Сатурном, Ураном и Нептуном.

На каждый рейс потребуется один космический корабль.

Сколько кораблей понадобится?