Выберите серию
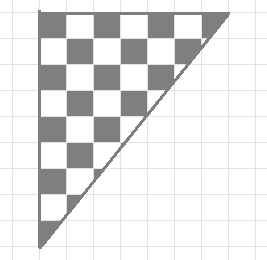
Чему равна суммарная площадь, окрашенная чёрным? (площадь клетки принимаем за 1)





Ответ:
Варианты ответов:
Перед нами - половина шахматной доски 7x9, разрезанной вдоль диагонали. Так как две половины симметричны относительно центра, в них поровну чёрного цвета. Поскольку всего на доске 7x9 - 32 чёрных клетки, ответом будет 16.
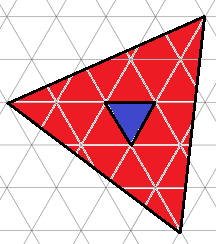
Во сколько раз площадь красной фигуры больше площади синей?





Ответ:
Варианты ответов:
Продолжив стороны синего треугольника, разрежем красную фигуру на три одинаковых "больших" треугольника. Два таких треугольника можно соединить так, чтобы получился параллельграмм со сторонами 2 и 3, площадь которого равна 2x3x2 = 12 (за единицу мы принимаем площадь синего треугольника). Таким образом, площадь "большого" треугольника равна 12:2 = 6, и значит, площадь красной фигуры равна 18.
При решении этой задачи полезно:
1) Ответить на вопрос: сколько синих треугольничков поместится в красную фигуру.
2) Обсудить основную идею при решении данной задачи – идея разрезания фигуры на более простые фигуры, из которых можно сложить фигуру, состоящую из целого числа единичных треугольников.
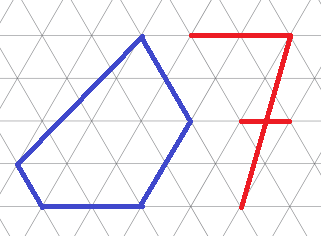
Длина единичного отрезка треугольной сетки равна 1. На сколько периметр синего "нуля" больше периметра красной "семерки"?





Ответ:
Варианты ответов:
Периметр синей фигуры состоит из "длинного отрезка" (равного дигонали параллелограмма, составленного из шести треугольничков сетки) и семи единичных отрезков сетки. Периметр красной фигуры состоит из такого же "длинного отрезка" и трех единичных отрезков сетки. Поэтому нужная нам разность периметров равна 4.
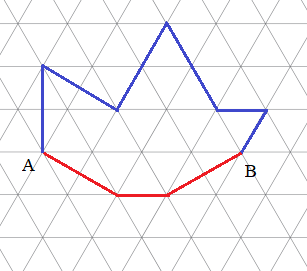
Катя и Саша встретились в точке А. Катя прошла в точку В по красному маршруту, а Саша пробежала в точку В по синему маршруту. На сколько метров маршрут Саши длиннее, если длина отрезка треугольной сетки между соседними узлами равна 200 метров?





Ответ:
Варианты ответов:
В маршруте Кати два "длинных отрезка" (длинные диагонали ромба, составленного из двух треугольничков сетки) и один "короткий" отрезок (единичный отрезок сетки). В маршруте Саши также два длинных отрезка и шесть коротких. Значит, маршрут Саши длиннее на 5 коротких отрезков, т.е. на 5x200 = 1000 метров.
При решении этой задачи полезно обсудить: так как нам нужно по сути найти разность периметров геометрических фигур (см. задачу 4), то основная идея решения подобных задач – идея поиска равных отрезков периметра, неудобных для нахождения в ситуации задачи, длины которых при вычитании взаимно уничтожатся.
Какова площадь зеленой фигуры (в квадратных сантиметрах), если известно, что площадь единичного треугольничка треугольной сетки равна 3 квадратных сантиметра?






Ответ:
Варианты ответов:
Фигура разбивается на 2 одинаковых треугольника и параллелограмм (посередине), состоящий из 2x3x2 = 12 единичных треугольничков. Из двух одинаковых треугольников составляется параллелограмм, состоящий из 1x3x2 = 6 единичных треугольничков. Итого закрашенная площадь равна площади 18 закрашенных треугольничков. В квадратных сантиметрах это 18x3 = 54.
Основная идея при решении этой задачи – это идея разбиения на «удобные» фигуры. То есть такие, которые содержат целое число единичных элементов фигуры (в нашем случае – единичных треугольников), или из которых при сложении можно получить фигуру, состоящую из единичных элементов.
Чтобы закрасить розовую "картину" понадобилось 3 тюбика розовой краски. А сколько таких же по объему тюбиков желтой краски уйдет на покраску желтой "рамки"?






Ответ:
Варианты ответов:
Прямоугольники разбиваются на треугольнички треугольной сетки и половинки таких треугольничков. Заметив это, несложно подсчитать, что и розовая, и желтая площади составляют 12 треугольничков. Значит, желтой краски потребуется столько же, сколько и розовой.
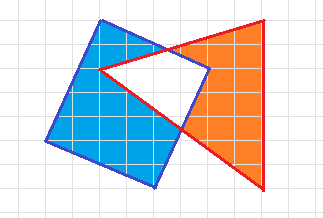
На сколько клеток площадь оранжевой фигуры меньше площади голубой?





Ответ:
Варианты ответов:
Добавим к фигурам общую часть – получим голубой четырехугольник и оранжевый треугольник. Вокруг четырехугольника опишем прямоугольник 6x7 со сторонами, идущими по линиям сетки, при этом добавлены по два прямоугольных треугольника с катетами 2 и 4, 2 и 5. Значит, площадь четырехугольника равна 6x7 - 2x4 - 2x5 = 24. У треугольника вертикальная сторона равна 7, а высота к этой стороне равна 6 значит его площадь равна 7x6 : 2 = 21. Итого, нужная нам разность площадей равна 3.
Нам нужно найти, на сколько площадь оранжевой фигуры меньше площади голубой, то есть фактически найти разность площадей SГ – SО. Заданные фигуры неправильной формы, площади которых неудобно вычислять. Но если добавить к каждой из них белый четырехугольник (значение площади которого при вычитании уничтожится), то получатся «хорошие» для вычисления площади треугольник и четырехугольник.
Таким образом первая идея, которая используется при решении этой задачи – идея добавления одной и той же (общей) части к фигурам, чтобы получить удобные для вычисления площади фигуры.
Площадь треугольника может быть найдена по основной формуле: полупроизведение стороны на высоту, проведенную к ней. И здесь вырисовывается еще одна идея, которая полезна при решении задач по геометрии: рассмотрение привычной фигуры в другой ориентации. Здесь мы треугольник рассматриваем в положении, когда сторона, к которой проводится высота, расположена вертикально, а не горизонтально.
Для нахождения площади бело-голубого четырехугольника может быть использована идея достраивания до удобной фигуры (прямоугольника, стороны которого проведены вертикально и горизонтально через вершины бело-голубого четырехугольника). Площадь построенного прямоугольника складывается из площади четырехугольника и четырех прямоугольных треугольников
В том случае, когда учащиеся еще не знают формулу площади произвольного треугольника, та же идея могут быть использованы и для нахождения площади оранжево-белого треугольника.
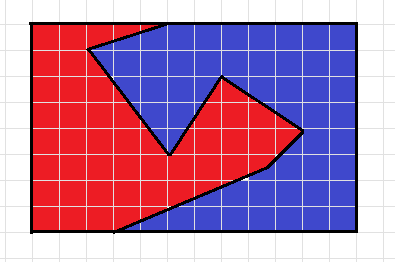
Чему равна разность периметров красной и синей фигур? (длину стороны клетки считаем равной 1)





Ответ:
Варианты ответов:
Часть границы внутри прямоугольника принадлежит обеим фигурам. Поэтому достаточно посчитать разность периметров, лежащих на границе прямоугольника. Видим, что эта разность равна 8.
Так как нам нужно найти разность периметров красной и синей фигуры, то основная идея при решении этой задачи – компенсация отрезков периметра красной и синей фигуры при вычитании.
При вычитании взаимно уничтожаются не только длины отрезков периметра, которые лежат внутри прямоугольника и принадлежат обеим фигурам, но и отрезки границы, которые ограничивают прямоугольник справа и слева. Поэтому достаточно найти разность отрезков периметров, расположенных на верхней и нижней части периметра прямоугольника.
Рекомендации:
Задать вопросы: что значит «найти разность периметров двух фигур»? Как это можно сделать? Обязательно ли для этого вычислять периметры обеих фигур по отдельности? Из каких отрезков состоит периметр каждой фигуры? Какие из этих отрезков принадлежат обеим фигурам? Какие из отрезков одинаковые?
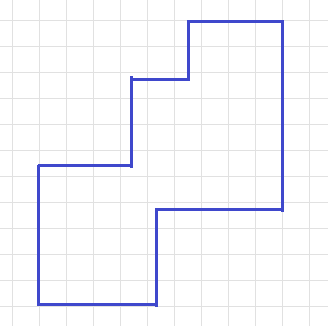
Найдите периметр многоугольника (длину стороны клетки принимаем за 1).





Ответ:
Варианты ответов:
Продолжив левую и правую границы, а также верхнюю и нижнюю границы, получим прямоугольник 9x11. Искомый периметр будет такой же, как у этого прямоугольника. Действительно, обойдем контур по часовой стрелке: вправо и влево мы прошли длину 9, а вверх и вних - длину 11.
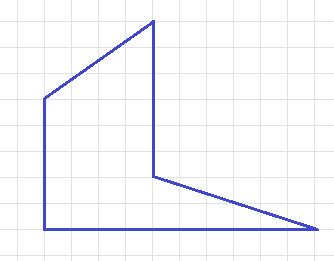
Чему равна площадь синего "сапога"? (площадь одной клетки принимаем за 1)





Ответ:
Варианты ответов:
Отрежем "справа" прямоугольный треугольник с катетами 2 и 6, и "сверху" - прямоугольный треугольник с катетами 3 и 4, останется прямоугольник 5x4. Итого площадь равна 2x6:2 + 3x4:2 + 5x4 = 32.
Забор (на плане показан зеленым) ограничивает шестиугольный участок. Найдите площадь этого участка (в квадратных метрах), если площадь одной клетки равна 25 кв. м.
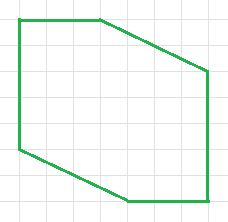





Ответ:
Варианты ответов:
Дополним участок до квадратного участка 7x7 (клеток), добавив два прямоугольных треугольника с катетами 2 и 4. Из двух таких треугольников можно сложить прямоугольник 2x4, значит добавленная площадь равна 8 клеток. Итого, площадь равна 49-8 = 41 клатку, или 41x25 = 1025 кв. м.