Восстановите решение задачи *раскраски07*.

*Условие задачи.*

_Докажите, что квадрат $6\times6$ нельзя разбить на прямые тетрамино._

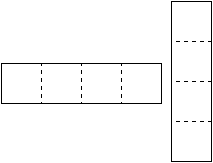
*Решение задачи.*

Пусть кто-то смог разбить квадрат $6\times6$ на прямые тетрамино.

Рассмотрим диагональную раскраску в 4 цвета. Каждая фигура тетрамино занимает при такой раскраске фиксированное количество белых клеток. А именно __.

Квадрат из 36 клеток должен разбиться ровно на __ фигурок из четырех клеток.

Заметим, что при выбранной раскраске, каждая такое тетрамино содержит в себе по 1 клетке каждого цвета.

Учитывая общее количество тетрамино, красных клеток должно быть __,

но согласно раскраске количество красных клеток равно __ .

Получили противоречие, значит невозможно разбить квадрат таким образом.