\justifying \large
\begin{frame} { делимость07 }
В следующем ряду чисел укажите числа, делящиеся на 3, но не делящиеся на 9:
а) 777777; б) 888; в) 567; г) 11011011; д) 73737.
\end{frame}\begin{frame} { Круги Эйлера - 01 }
Каждая из 20 машинок - либо красная, либо быстрая, либо и красная, и быстрая. Красных машинок 13, быстрых - 11. Сколько машинок являются и красными, и быстрыми?
\end{frame}\begin{frame} { Логические операции-02n }
Для каких n утверждение
<<Число n делится на 3 и не делится на 2>>
истинно?
\end{frame}\begin{frame} { разное40 }
Придумайте пять различных двузначных нечётных чисел с суммой 77. В ответ запишите самое большое и самое маленькое из них. Только два числа!
\end{frame}\begin{frame} { раскраски011 }
С помощью раскраски покажите, что если вырезать клетку B или C, то остаток не получится разрезать на полоски 1х3.
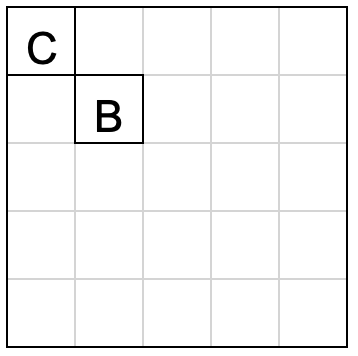
Выберите раскраски, которые могут помочь в этом.




\begin{frame} { РиЛ-01 }
Собрались двое островитян. Первый сказал: "Мы оба лжецы". Кто из них кто?
Первый __
Второй __
\end{frame}\begin{frame} { РиЛ-10 }
В комнате три островитянина. Первый сказал: «В комнате один рыцарь», второй ответил: «Нет, в комнате два рыцаря!», третий заявил: «В комнате все рыцари!». Сколько рыцарей может быть в комнате?
\end{frame}\begin{frame} { факториал05 }
Заполните пропуски в решении задачи "Сколькими способами можно поставить в ряд 10 человек?". Есть __ вариантов поставить кого-то на первое место. После этого есть __ вариантов поставить кого-то на второе место. Эти числа нужно __, потому то на каждый из вариантов поставить первого есть __ вариантов поставить второго. На третье место есть __ вариантов поставить человека, и т.д. Получается ответ: __
\end{frame}\begin{frame} { фигуры02 }
Задача: Можно ли поставить на доске $3 \times 4$ четыре ладьи чтобы они не били друг друга?
Заполните пропуски в решении:
Ответ: __. Пусть у нашей доски __ строки и __ столбца. Заметим, что в каждой __ стоит не более __ ладьи, следовательно ладей на доске не больше чем __ ладьи и 4 их быть не может.
\end{frame}